Model과 Gradient Descent

모델(Model)이란 무엇인가?

요즘 개발자들 사이에서 가장 핫한 키워드는 단연 'AI'와 '모델'입니다. 흔히 "모델을 학습시킨다"라고 하는데, 여기서 모델은 도대체 무엇일까요?

개발자 관점에서 모델은 '특정 정보를 입력을 받아 연산을 거쳐 그정보에 따라 원하는 값을 예측값을 출력하는 함수'로 정의할 수 있습니다. 중고등학교 수학 시간에 지겹도록 봤던 $y = f(x)$가 바로 모델의 본질입니다.

오늘은 가장 기초적인 선형 회귀(Linear Regression) 모델을 직접 구현해보며, 기계가 데이터를 통해 어떻게 '학습'을 하는지 그 원리를 파헤쳐 보겠습니다.

 

우리는 오늘 다음과 같은 문제를 해결하는 모델을 만들어볼 것입니다.

"맥북의 사용 연수($x$)를 입력받아, 중고 가격($y$)을 예측해보자!"

가장 직관적이고 간단한 모델은 직선 형태인 일차 함수일 것입니다.

$$y = wx + b$$

• $x$ (Input): 사용 연수 (특성, Feature)
• $y$ (Output): 중고가 (타겟, Target)
• $w$ (Weight, 가중치): 기울기. 연식이 가격에 얼마나 큰 영향을 미치는지 나타내는 값
• $b$ (Bias, 편향): $y$절편. 연식이 0일 때의 기본 가격

우리의 목표는 데이터($x, y$)를 가장 잘 설명하는 $w$와 $b$를 찾아내는 것입니다.

 

학습(Training)의 본질: 방정식 풀기

"모델을 학습시킨다"라는 말은 아주 거창해 보이지만, 사실 수학적으로는 "최적의 $w$와 $b$를 구하는 방정식 풀이"와 같습니다.

이해를 돕기 위해, 세상에 맥북 중고 거래 데이터가 딱 2개만 있고, 이 데이터가 절대적인 진리라고 가정해 봅시다.

• 데이터 1: 2년 쓴 맥북이 100만 원에 팔림 ($x=2, y=100$)
• 데이터 2: 5년 쓴 맥북이 40만 원에 팔림 ($x=5, y=40$)

이 규칙을 완벽하게 만족하는 모델($w, b$)을 찾으려면 어떻게 해야 할까요? 우리는 중학교 때 배운 연립방정식을 세울 수 있습니다.

$$\begin{cases} 100 = w \times 2 + b \\ 40 = w \times 5 + b \end{cases}$$

이 두 식을 연립해서 풀면 $w$와 $b$가 툭 튀어나옵니다.

1. 위 식에서 아래 식을 빼면: $60 = -3w \rightarrow w = -20$
2. $w$를 대입하면: $100 = -40 + b \rightarrow b = 140$

결과: $y = -20x + 140$

• 해석: 맥북은 새 제품이 140만 원이고, 1년 지날 때마다 20만 원씩 가격이 떨어진다.

자, 이렇게 $w$와 $b$를 구했습니다. 이제 "6년 된 맥북($x=6$)"이 얼마인지 물어보면, $y = -20(6) + 140 = 20$, 즉 20만 원이라는 답을 낼 수 있습니다. 이것이 바로 학습의 완료입니다.

 

현실의 데이터: 변수가 하나가 아니라면? (다변수 선형 회귀)

앞서 본 맥북 예제($x$가 1개)는 아주 이상적인 상황이었습니다. 현실 세계의 데이터는 훨씬 복잡하죠.

이번에는 식당의 팁(Tip) 예측 문제를 예로 들어보겠습니다.

우리가 가진 데이터셋에는 total_bill(총 식대), time_Dinner(저녁 시간 여부), size(인원 수) 등 총 12가지의 정보(Feature)가 있다고 가정해 봅시다. 그리고 이 12가지 정보를 조합해 손님이 지불할 팁($y$)을 예측해야 합니다.

이전에는 입력 데이터($x$)가 '사용 연수' 하나였기에 모델이 단순했습니다.

$$y = wx + b$$

하지만 이번에는 $x$가 무려 12개입니다! 그렇다면 우리의 모델은 어떻게 변해야 할까요? 아주 자연스럽게 확장하면 됩니다.

$$y = w_1x_1 + w_2x_2 + w_3x_3 + \dots + w_{12}x_{12} + b$$

• $x_1, x_2, \dots, x_{12}$: 총 식대, 인원 수 등 12개의 입력 정보
• $w_1, w_2, \dots, w_{12}$: 각 정보가 팁에 미치는 영향력(가중치)
• $b$: 기본 편향

식이 길어 보이지만 본질은 간단합니다. "각 입력값($x$)에 알맞은 가중치($w$)를 곱해서 전부 더한다"는 것이죠.

개발자분들이라면 이 긴 식을 더 우아하게 표현하고 싶으실 겁니다. 우리는 이것을 벡터의 내적(Dot Product)으로 표현할 수 있습니다.

$$y = \mathbf{w}^T\mathbf{x} + b$$

데이터가 아무리 많아져도 원리는 동일합니다. 모델 학습의 목표는 12개의 $x$들과 팁($y$) 사이의 관계를 가장 잘 설명해주는 최적의 $w$ 세트($w_1$부터 $w_{12}$)와 $b$를 찾아내는 것입니다.

 

이것을 선형 방정식이라고 합니다. 다른 말로는 "다변수 일차방정식"이라고 합니다.

선형 회귀는 선형 방정식 을 통해 회귀 문제를 푼다 는 의미가 담겨 있습니다., 이 중 특히 회귀(Regression) 라는 단어는 연속된 실수값을 예측하는 문제 를 뜻합니다. 회귀와 대립되는 개념은 분류 인데, 다음 예를 보면 가볍게 이해가 되실 겁니다.

• 사진을 입력받아 해당 사진이 강아지인지, 고양이인지 맞히는 문제는 분류 문제입니다.
• 사용연수, 화면크기 등을 입력받아 실수값인 중고 가격을 맞히는 문제는 회귀 문제입니다.

즉, 분류 문제는 맞히고자 하는 값이 카테고리 이고, 회귀 문제는 맞히고자 하는 값이 연속된 실수 값 입니다.

 

현실의 벽: 오차(Error)의 발생

하지만 현실 세계의 데이터는 이렇게 깔끔하지 않습니다. 같은 2년 쓴 맥북이라도 흠집에 따라 90만 원일 수도, 110만 원일 수도 있습니다. 데이터가 수백, 수천 개라면 모든 점을 완벽하게 지나는 하나의 직선은 존재할 수 없습니다.

그래서 머신러닝의 목표는 '완벽한 정답'을 찾는 것이 아니라, "오차가 가장 적은 최선의 직선(Best Fit)"을 찾는 것으로 바뀝니다.

이때 모델이 얼마나 잘하고 있는지를 채점하는 점수표가 필요한데, 이를 손실 함수(Loss Function)라고 부릅니다. 아직 불안정한 현재의 모델이 출력하는 값과 실제 정답간의 차이를 확인한다.

$$RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n} (y_{예측} - y_{실제})^2}$$

• 차이(Error): 예측값과 실제값의 차이를 구합니다.
• 제곱(Square): 차이가 양수/음수 섞여서 0이 되는 것을 막고, 큰 오차에 더 큰 페널티를 줍니다.
• 평균(Mean) & 루트(Root): 데이터 개수로 나누고, 제곱된 단위를 다시 원래 가격 단위로 돌려놓습니다.

결론: 이 Loss 값을 0에 가깝게 최소화하는 $w, b$를 찾는 것이 머신러닝 학습의 최종 목표입니다.

 

보통 RMSE는 사람이 확인할때 쓰고, 손실함수는 MSE를 모델이 학습할때 많이 사용합니다.

 

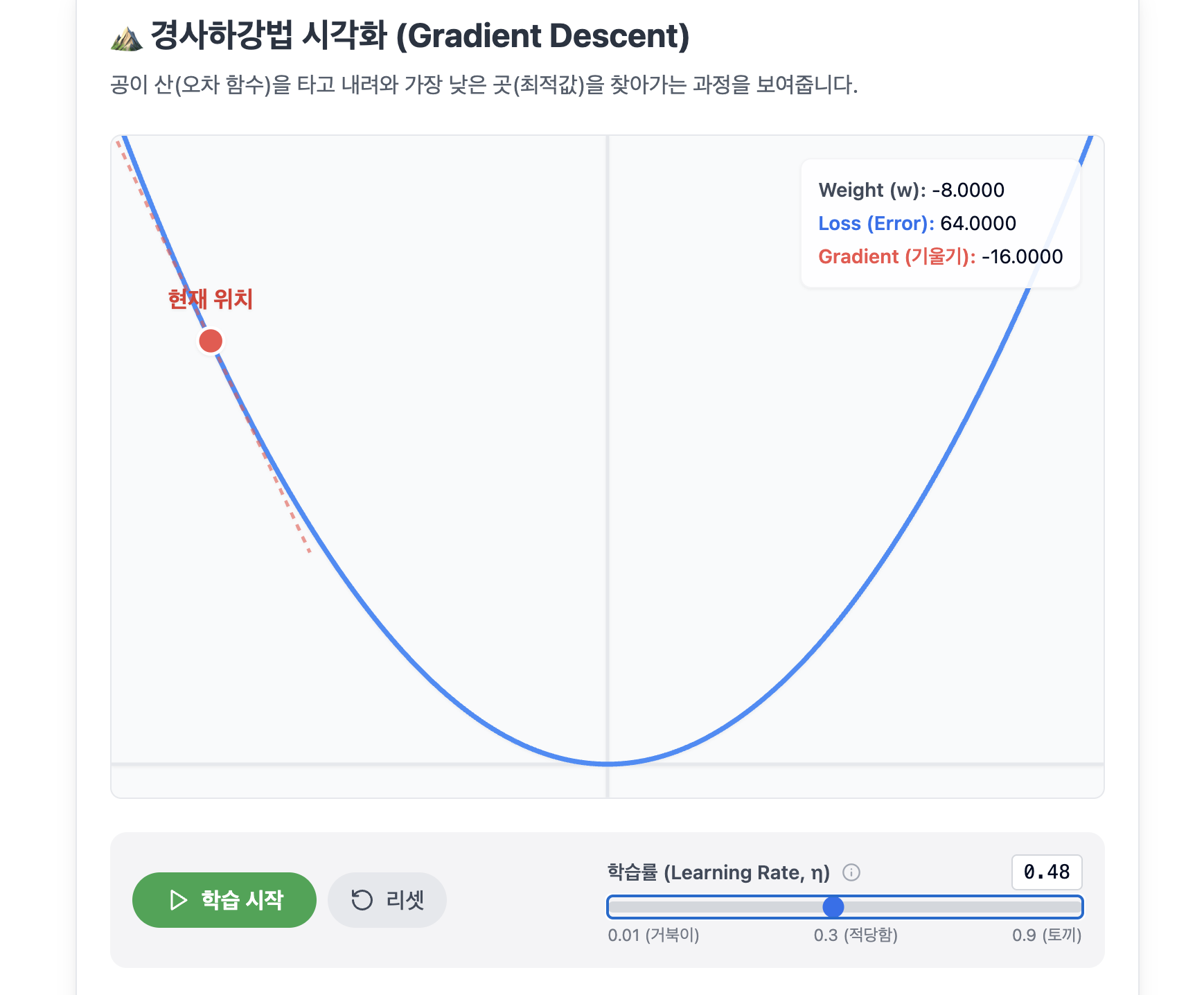
모델을 똑똑하게: 경사하강법(Gradient Descent)

우리는 최적의 $w, b$를 모르기 때문에, 처음에는 아무 값이나 랜덤으로 넣고 시작합니다. 당연히 오차(Loss)가 엄청나게 클 것입니다.

이때 오차를 줄이는 방향으로 $w$와 $b$를 조금씩 수정해 나가는 방법을 경사하강법이라고 합니다.

 

미분값의 정의

수학에서 기울기($\frac{dy}{dx}$)가 의미하는 바는 아주 명확합니다.

"x(입력)를 아주 조금 증가시켰을 때, y(오차)는 어떻게 변하는가?"

이 정의에 따라 두 가지 상황이 나옵니다.

• 상황 A: 발끝이 들려 있다 (오르막길 )
  • 상태: 기울기가 양수(+)입니다.
  • 의미: "$x$를 증가시키면 $\rightarrow$ $y$(오차)도 커진다(증가한다)."
  • 우리의 목표: 오차($y$)를 줄여야 합니다.
  • 행동: $x$를 증가시키면 오차가 커진다고 하니, 반대로 $x$를 줄여야(뒤로 가야) 합니다.
• 상황 B: 발끝이 내려가 있다 (내리막길 )
  • 상태: 기울기가 음수(-)입니다.
  • 의미: "$x$를 증가시키면 $\rightarrow$ $y$(오차)는 작아진다(감소한다)."
  • 우리의 목표: 오차($y$)를 줄여야 합니다.
  • 행동: $x$를 증가시켰더니 오차가 작아지네? 그럼 계속 $x$를 늘려야(앞으로 가야) 합니다.

이를 수식으로 표현하면 파라미터 업데이트 공식이 됩니다.

$$w_{new} = w_{old} - \eta \times \frac{\partial Loss}{\partial w}$$

• $\frac{\partial Loss}{\partial w}$ (기울기, Gradient): 미분을 통해 구합니다. 현재 위치에서 오차가 커지는 방향을 알려줍니다.
• $-$ (빼기): 기울기가 가리키는 방향의 반대로 가야 산을 내려갈 수 있습니다.
• $\eta$ (학습률, Learning Rate): 한 번에 발을 얼마나 넓게 디딜지 정하는 값입니다. 너무 작으면 내려가는 데 한세월이 걸리고, 너무 크면 골짜기를 지나쳐버릴 수 있습니다.
  어떤 학습률을 사용하는 것이 가장 좋은지는 실제로 실험을 해 보기 전까지는 모릅니다. 이렇게 학습률과 같이 모델이 스스로 학습해나가는 파라미터 가 아니라, 사람이 직접 사전에 정하고 시작해야 하는 파라미터 를 하이퍼 파라미터 라고 합니다.
  사실 복잡한 데이터셋에서는 보통 학습률을 0.0001 ~ 0.01 정도의 작은값을 사용합니다.
  
  가장 기본적인 선형 회귀의 경우, 가중치에 대한 미분값(기울기)은 연쇄 법칙(Chain Rule)에 의해 다음과 같은 형태가 됩니다.
  $$\frac{\partial \text{Loss}}{\partial w} = (\text{예측값} - \text{실제값}) \times x$$
  이 수식을 바탕으로 문제의 텍스트를 단계별로 해석하면 이렇습니다:
  • 특징값($x$)이 작음: 예를 들어 $x$가 $0.01$이라고 가정해 봅시다.
  • 기울기 계산: 오차(예측-실제)가 아무리 커도, 마지막에 $x$($0.01$)를 곱하게 되므로 기울기 자체가 작아집니다.
  • 학습률 반영: 이미 작아진 기울기에, 보통 작은 값인 학습률($0.001$)을 또 곱합니다.
  • 결과: $0.01 \times 0.001 = 0.00001$.
  • 최종 업데이트: 가중치 $w$는 기존 값에서 겨우 $0.00001$만큼만 이동합니다.
    x값이 작은 경우는 학습률도 같이 작게하면 학습의 효율이 극도로 떨어지게 됩니다.

 

 

 

순전파(Forward)와 역전파(Backward)

우리는 방금 수식과 미분을 통해 학습의 원리를 배웠습니다. 이제 이 과정을 AI 개발자들이 사용하는 '전문 용어'로 매핑해 보겠습니다. 딥러닝이나 머신러닝 논문을 보면 항상 나오는 Forwarding과 Backpropagation이 바로 이것입니다.

1. 순전파 (Forward Propagation)

• 개념: 입력 데이터($x$)를 모델에 넣어 예측값($y$)을 뽑아내는 과정입니다.
• 우리의 식: $y = \mathbf{w}^T\mathbf{x} + b$ 를 계산하는 단계가 바로 순전파입니다.
• 비유: 시험 문제를 풀어서 답안지를 제출하는 과정.

2. 역전파 (Backpropagation)

• 개념: 예측값과 정답 사이의 오차(Loss)를 구한 뒤, 반대로 거슬러 올라가며 가중치($w$)를 수정하는 과정입니다.
• 우리의 식: $\frac{\partial Loss}{\partial w}$ (기울기)를 계산하고, $w_{new} = w_{old} - \eta \times \text{기울기}$ 공식을 적용하는 단계입니다.
• 비유: 채점 후 틀린 문제를 분석하여 지식(가중치)을 고치는 오답 노트 과정.

결국 "모델을 학습시킨다"는 것은 순전파(문제 풀기)와 역전파(지식 수정)를 끊임없이 반복하는 루프(Loop)를 돌리는 것입니다.

 

전체적인 과정

우리가 준비한 입력 데이터($x$)와 정답 데이터($y$)가 실제 학습 과정에서 어떻게 쓰이는지 순서대로 살펴보겠습니다.

1. 초기화 (Initialization)
   • $w$(가중치)와 $b$(편향)를 랜덤한 값으로 설정합니다.
2. 순전파 (Forward Propagation)
   • 입력($x$) 투입: 현재의 $w, b$ 모델에 $x$를 넣습니다.
   • 예측: 모델이 계산을 수행하여 예측값($y_{pred}$)을 내놓습니다.
   • (참고: 여기까지는 정답 $y$를 보지 않고 모델 혼자서 답을 추측하는 단계입니다.)
3. 오차 계산 (Loss Calculation) $\leftarrow$ 정답($y$) 등장!
   • 채점: 방금 구한 예측값($y_{pred}$)과 실제 정답($y_{true}$)을 비교합니다.
   • 계산: 둘의 차이를 제곱하거나 평균을 내어 손실함수 값(Loss)을 구합니다.
   • (핵심: 모델이 얼마나 틀렸는지 확인하는 이 순간, 비로소 정답 데이터가 사용됩니다.)
4. 역전파 (Backpropagation)
   • 원인 분석: 계산된 손실(Loss)을 줄이기 위해, 미분을 사용하여 각 가중치($w$)가 오차에 미친 영향(기울기, Gradient)을 계산합니다.
   • 오차를 역방향으로 전파하며 수정할 방향을 찾습니다.
5. 가중치 업데이트 (Optimization)
   • 구해진 기울기(Gradient)를 바탕으로 파라미터를 실제로 수정합니다.
   • $w' = w - \eta \times \text{기울기}$
   • $b' = b - \eta \times \text{기울기}$
6. 반복 (Iteration)
   • 손실(Loss)이 충분히 줄어들 때까지 2~5번 과정을 계속 반복합니다.