데이터 전처리: Outlier 탐지와 처리: Z-Score부터 IQR까지

데이터 분석과 머신러닝 모델의 성능을 결정짓는 것은 결국 '데이터의 품질'입니다. 그중에서도 이상치(Outlier)는 모델을 왜곡시키고 분석 결과를 편향되게 만드는 주범이죠. 오늘은 이상치의 개념부터 대표적인 탐지 방법인 Z-Score와 IQR의 원리, 그리고 파이썬 구현법까지 자세히 알아보겠습니다.

 

Outlier란 무엇인가?

이상치란 대부분의 값들이 모여 있는 범위에서 크게 벗어난, 극단적으로 크거나 작은 값을 의미합니다.

무역(Trade) 데이터를 예로 들어봅시다. 대부분의 거래 금액이 100~1,000만 원 사이인데, 갑자기 1,000억 원짜리 거래 데이터가 하나 섞여 있다고 가정해 보겠습니다.

1. 스케일링의 왜곡: Min-Max Scaling을 적용하면 1,000억 원이 1이 되고, 나머지 일반적인 데이터들은 모두 0에 아주 가까운 값으로 수렴해 버립니다. 데이터 간의 유의미한 차이가 사라지는 것이죠.
2. 모델의 편향: 선형 회귀와 같은 모델은 평균값에 민감하게 반응하므로, 단 몇 개의 이상치 때문에 모델 전체가 엉뚱한 방향으로 학습될 수 있습니다.

---

Outlier 탐지

Z-Score (표준 점수) 방법

 데이터가 평균으로부터 표준편차의 몇 배만큼 떨어져 있는지를 나타내는 지표입니다. 데이터가 정규분포를 따른다고 가정할 때 사용합니다.

$$z = \frac{X - \mu}{\sigma}$$

• $\mu$: 평균
• $\sigma$: 표준편차

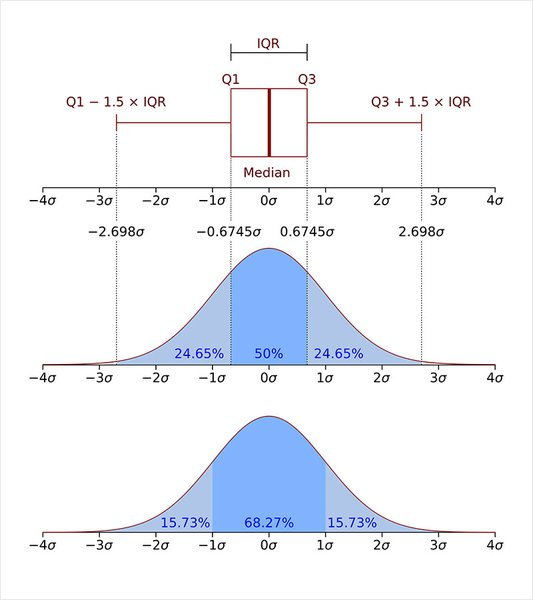
일반적으로 |Z| > 3 (평균에서 표준편차의 3배 이상 떨어진 값)인 데이터를 이상치로 판단합니다. (통계적으로 정규분포에서 데이터의 99.7%가 $\pm3\sigma$ 안에 들어오기 때문입니다.)

 

IQR (Interquartile Range) 방법

Z-Score는 평균을 사용하기 때문에 이상치 자체에 영향을 많이 받는다는 단점이 있습니다. 이를 보완하기 위해 사분위수를 이용한 IQR 방식을 널리 사용합니다.

 

데이터를 크기순으로 나열했을 때 25%(Q1), 50%(Q2, 중앙값), 75%(Q3) 지점의 값을 이용합니다.

• IQR: $Q3 - Q1$ (중간 50% 데이터가 퍼져 있는 범위)
  • Q1 (1사분위수): 전체 데이터 중 하위 25% 지점의 값
  • Q2 (2사분위수): 중앙값 (Median, 50% 지점)
  • Q3 (3사분위수): 전체 데이터 중 상위 25% 지점의 값
• Lower Bound (하한선): $Q1 - 1.5 \times IQR$
• Upper Bound (상한선): $Q3 + 1.5 \times IQR$

 

 

Z-Score vs IQR: 무엇이 다른가?

Z-Score 방법에는 두 가지 뚜렷한 한계점이 있습니다.

1. Robust(강건)하지 못함: Z-Score의 계산 공식에는 평균($\mu$)과 표준편차($\sigma$)가 들어갑니다. 하지만 평균과 표준편차 자체가 이상치에 매우 민감합니다. 이상치가 너무 크면 평균을 자기 쪽으로 끌어당겨서, 정작 본인은 "평균과 별로 안 먼데?"라고 판정되는 오류(Masking effect)가 발생할 수 있습니다. 반면 IQR은 중앙값을 사용하므로 이상치에 훨씬 강건합니다.
2. 소규모 데이터셋에서의 한계: 데이터 개수가 너무 적으면(대략 12개 이하) 통계적으로 Z-Score가 특정 임계값을 넘지 못하는 경우가 발생하여 이상치를 탐지하는 것이 수학적으로 불가능해질 수 있습니다.

---

이상치를 찾은 후 어떻게 처리할까?

이상치를 발견했다고 해서 무조건 삭제하는 것이 정답은 아닙니다.

• 삭제 (Deletion): 이상치가 단순 기입 오류이거나 분석 대상을 방해하는 노이즈일 때 사용합니다.
• 대체 (Imputation): 데이터가 부족할 경우 삭제 대신 최솟값/최댓값(Capping/Flooring)으로 변환하거나, 중앙값 등으로 대체합니다.
• 예측 모델 활용: 결측치 처리와 마찬가지로 다른 변수들을 활용해 "이 데이터가 정상이었다면 가졌을 값"을 예측하여 채워넣습니다.
• 범주화 (Binning): 수치형 데이터를 구간별로 나누어 범주형으로 변환함으로써 이상치의 절대적인 수치 영향을 줄입니다.