Loss Function

오늘은 딥러닝 모델의 성능을 결정짓는 핵심 요소, 손실 함수(Loss Function)에 대해 깊이 있게 알아보겠습니다. 단순히 종류를 나열하는 것에 그치지 않고, 각 함수가 어떤 수학적 원리로 모델을 학습시키는지 정리해 보았습니다.

 

손실 함수란 무엇인가?

"모델의 오답을 수치화하여 나아갈 방향을 제시하는 채점표"

 

모델의 학습 과정은 결국  손실 함수의 값을 최소화(Minimize)하는 과정입니다. 손실 함수는 현재 모델의 예측값($\hat{y}$)과 실제 정답($y$) 사이의 거리를 측정합니다. 이 거리가 멀수록(손실이 클수록) 모델은 가중치($w$)를 더 크게 수정하게 됩니다.

 

회귀(Regression) Task: 연속적인 숫자 맞추기

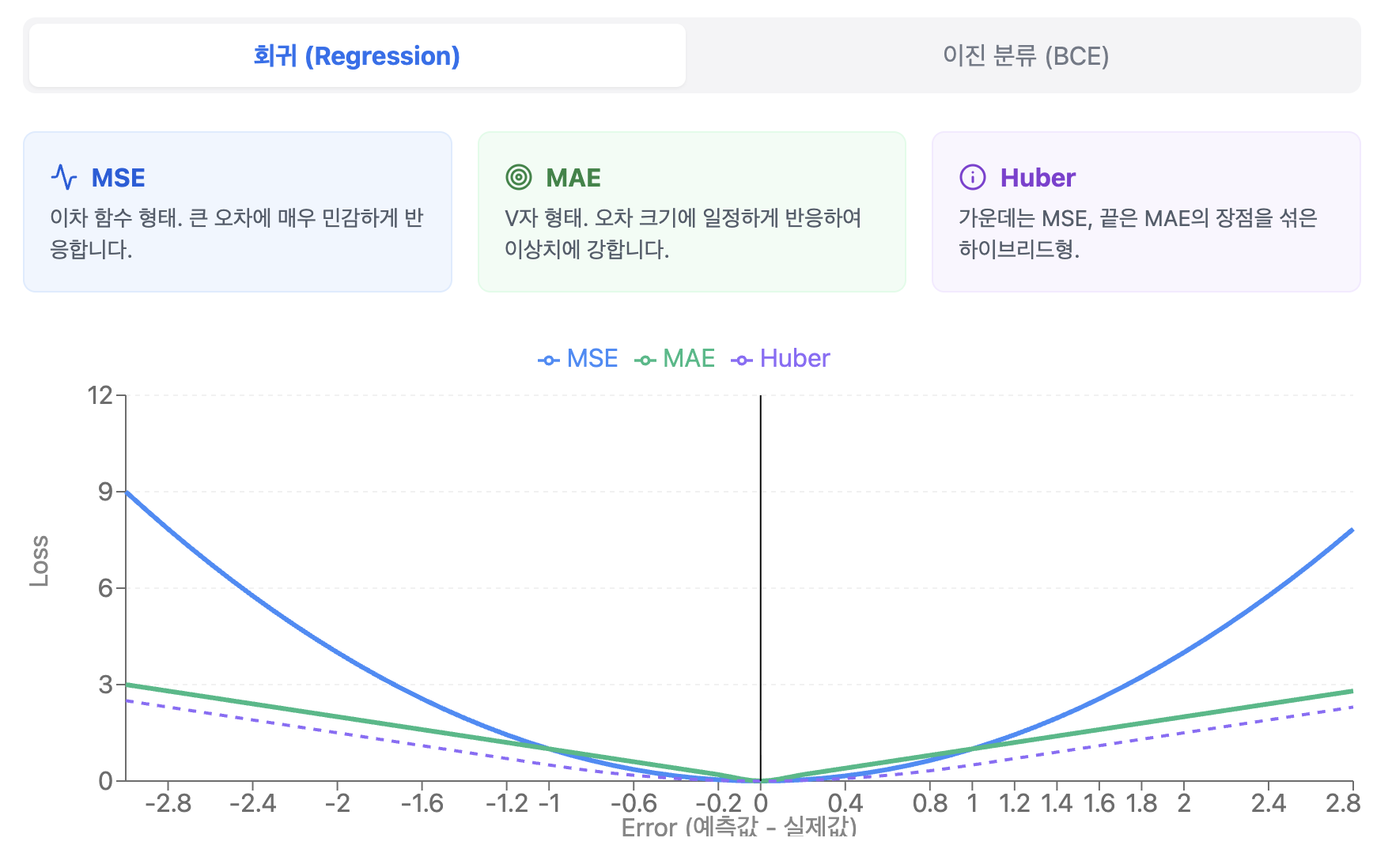
회귀에서의 핵심은 "실제 값과 예측 값 사이의 거리(Distance)"를 어떻게 정의하느냐입니다.

MSE (Mean Squared Error, 평균 제곱 오차)

• 원리: 오차를 제곱하여 평균을 냅니다.
• 수학적 특징: $MSE = \frac{1}{n} \sum (y - \hat{y})^2$
• 심층 분석: 제곱을 하기 때문에 오차가 1보다 크면 손실값이 기하급수적으로 커집니다. 이는 모델에게 **"작은 오차는 어느 정도 봐주겠지만, 큰 오차(실수)는 절대 용납하지 않겠다"**는 강력한 패널티를 부여하는 것과 같습니다.
• PyTorch 인자: nn.MSELoss

MAE (Mean Absolute Error, 평균 절대 오차)

• 원리: 오차의 절댓값을 취해 평균을 냅니다.
• 수학적 특징: $MAE = \frac{1}{n} \sum |y - \hat{y}|$
• 심층 분석: 모든 오차를 선형적으로 반영합니다. 즉, 이상치(Outlier)가 발생해도 MSE처럼 손실값이 폭발하지 않습니다. 데이터에 노이즈가 많거나 이상치에 민감하게 반응하지 않아야 할 때(Robustness) 주로 사용합니다.
• PyTorch 인자: nn.L1Loss

Huber Loss (MSE + MAE의 조화)

• 원리: 오차가 작을 때는 MSE를, 클 때는 MAE를 적용합니다.
• 심층 분석: MSE의 장점인 '부드러운 최적화'와 MAE의 장점인 '이상치에 대한 강인함'을 모두 가집니다. 학습 초기에는 빠르게, 최적값 근처에서는 안정적으로 수렴하도록 돕습니다.
• PyTorch 인자: nn.HuberLoss

---

분류(Classification) Task: 카테고리 맞추기

분류에서는 단순히 거리를 재는 것보다, "정답일 확률을 얼마나 확신하는가"가 중요합니다.

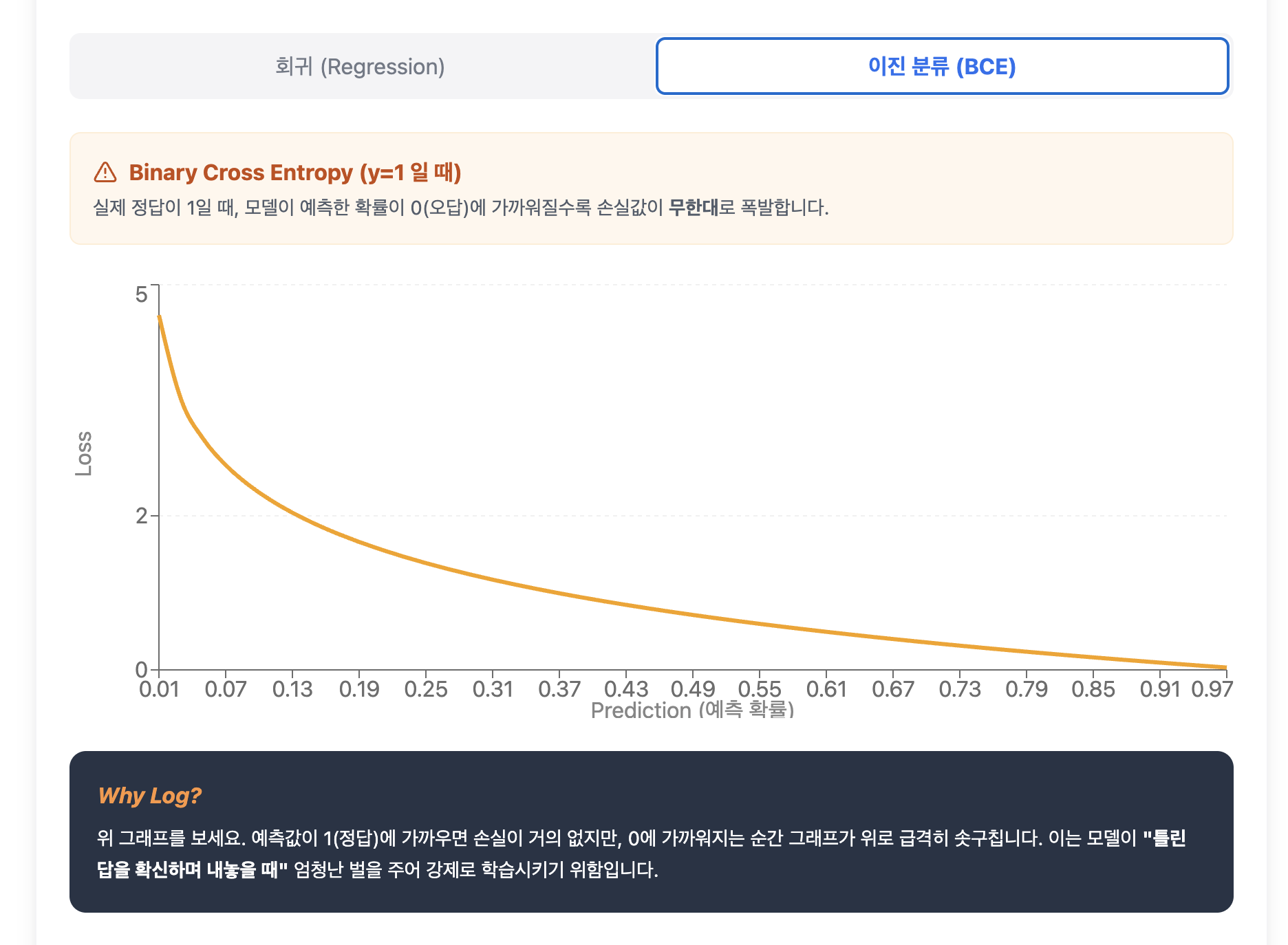
Binary Cross Entropy (BCE)

• 원리: 두 개의 클래스(0 또는 1)를 분류할 때 사용합니다.
• 수학적 특징: $Loss = -[y \log(\hat{y}) + (1-y) \log(1-\hat{y})]$
• 심층 분석: 로그($\log$) 함수를 사용하는 것이 핵심입니다. 모델이 정답을 0%에 가깝게 예측하면 손실값이 무한대로 발산합니다. 즉, "정답을 틀리는 것도 모자라, 오답을 확신하는 경우"에 엄청난 벌금을 매겨 모델이 확률을 정답 쪽으로 강하게 밀어내게 만듭니다.
• PyTorch 인자: nn.BCELoss (또는 Sigmoid가 포함된 nn.BCEWithLogitsLoss)

Cross Entropy (CE)

• 원리: 3개 이상의 클래스를 분류할 때 사용합니다.
• 심층 분석: Softmax 함수를 통해 나온 확률 분포와 실제 정답(One-hot vector)의 분포를 비교합니다. 두 분포가 다를수록 '정보 엔트로피'가 높아진다는 원리를 이용하여, 모델의 예측 분포가 실제 정답 분포와 일치하도록 유도합니다.
• 데이터의 범주가 $n$개일때 
  $$H(P, Q) = -\sum_{i=1}^{n} P(x_i) \log(Q(x_i))$$
  
  • $P(x_i)$: 실제 정답(Target)의 확률 (보통 원-핫 인코딩된 값: 0 또는 1)
  • $Q(x_i)$: 모델이 예측한 확률 (Softmax를 통과한 $0 \sim 1$ 사이의 값)

• PyTorch 인자: nn.CrossEntropyLoss

성능을 극대화하는 실전 "특수 손실 함수"

기본적인 MSE나 Cross Entropy만으로 해결되지 않는 복잡한 실전 문제(데이터 불균형, 이상치, 유사도 등)를 해결하기 위한 강력한 도구들입니다.

이름	주요 Task	핵심 원리 및 특징	비고 (강점)
Focal Loss	객체 탐지, 불균형 분류	어려운 문제에 집중. 맞추기 쉬운 샘플의 손실은 낮추고, 헷갈리는 샘플에 가중치를 두어 학습 효율 극대화.	클래스 불균형 해소
Cosine Similarity	추천 시스템, 얼굴 인식	방향의 일치. 값의 크기(L2 Norm)가 아닌 데이터 간의 '각도'를 계산하여 취향이나 의미적 유사성 판단.	데이터 크기에 무관
KL-Divergence	생성 모델 (VAE), Distillation	분포의 닮음. 모델이 예측한 확률 분포가 실제 정답 분포와 얼마나 '비슷한 모양'인지 측정.	확률 분포 최적화
Log-Cosh Loss	회귀 (Regression)	오차가 작으면 MSE, 크면 MAE처럼 동작하는 부드러운 함수.	이상치(Outlier)에 강함
Quantile Loss	수요 예측, 시계열	평균이 아닌 상위/하위 특정 분위수를 예측하여 미래의 불확실한 범위를 산출.	예측 구간 확보
Dice Loss	의료 영상 분할	예측 영역과 실제 영역의 교집합 비율을 직접 계산. 배경이 압도적으로 많을 때 효과적.	세그멘테이션 특화
Triplet Loss	유사도 학습 (Metric Learning)	기준(Anchor) 데이터와 같은 것은 가깝게, 다른 것은 멀게 만들어 공간적 배치를 학습.	특징 추출(Embedding)

 

 

데이터가 깔끔하면 MSE/CE면 충분하지만,

• 현실의 데이터는 이상치가 날뛰고(→ Log-Cosh),
• 정답 비율이 깨져 있으며(→ Focal/Dice),
• 때로는 단순한 값보다 범위가 중요합니다(→ Quantile).