딥러닝의 심장: 체인룰(Chain Rule)과 역전파(Backpropagation) 완벽 정리

 

딥러닝 모델이 수만, 수백만 개의 파라미터를 가지고 있음에도 어떻게 정확하게 학습될 수 있을까요? 그 비밀은 바로 체인룰(Chain Rule, 연쇄 법칙)을 이용한 역전파(Backpropagation) 알고리즘에 있습니다. 오늘은 이 두 개념의 정의와 작동 원리를 정리해 보겠습니다.

체인룰 (Chain Rule, 연쇄 법칙): 수학적 토대

체인룰은 합성함수의 미분을 계산하는 방법입니다. 여러 함수가 연결되어 있을 때, 최종 출력의 변화량을 입력부터 단계별 변화량의 곱으로 표현할 수 있다는 원리입니다.

수학적 정의

함수 $y = f(u)$와 $u = g(x)$가 있다고 가정하면, $x$에 대한 $y$의 미분은 다음과 같습니다.

$$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$$

직관적 이해: "최종 목적지($y$)의 변화량은 거쳐온 정거장($u$)에서의 변화율들을 모두 곱한 것과 같다."

역전파 (Backpropagation): 알고리즘적 구현

역전파는 체인룰을 신경망에 적용하여 손실 함수(Loss Function)의 기울기(Gradient)를 효율적으로 계산하는 알고리즘입니다.

학습의 3단계 흐름

1. 순전파 (Forward Pass): 입력 데이터를 넣고 층(Layer)을 통과시켜 예측값과 오차($L$)를 계산합니다.
2. 역전파 (Backward Pass): 출력층에서 발생한 오차를 입력층 방향으로 거꾸로 전파하며 각 가중치($w$)의 미분값을 구합니다.
3. 가중치 업데이트 (Update): 구해진 미분값(기울기)을 바탕으로 경사하강법(Optimizer)을 사용하여 가중치를 수정합니다.

 

 

 

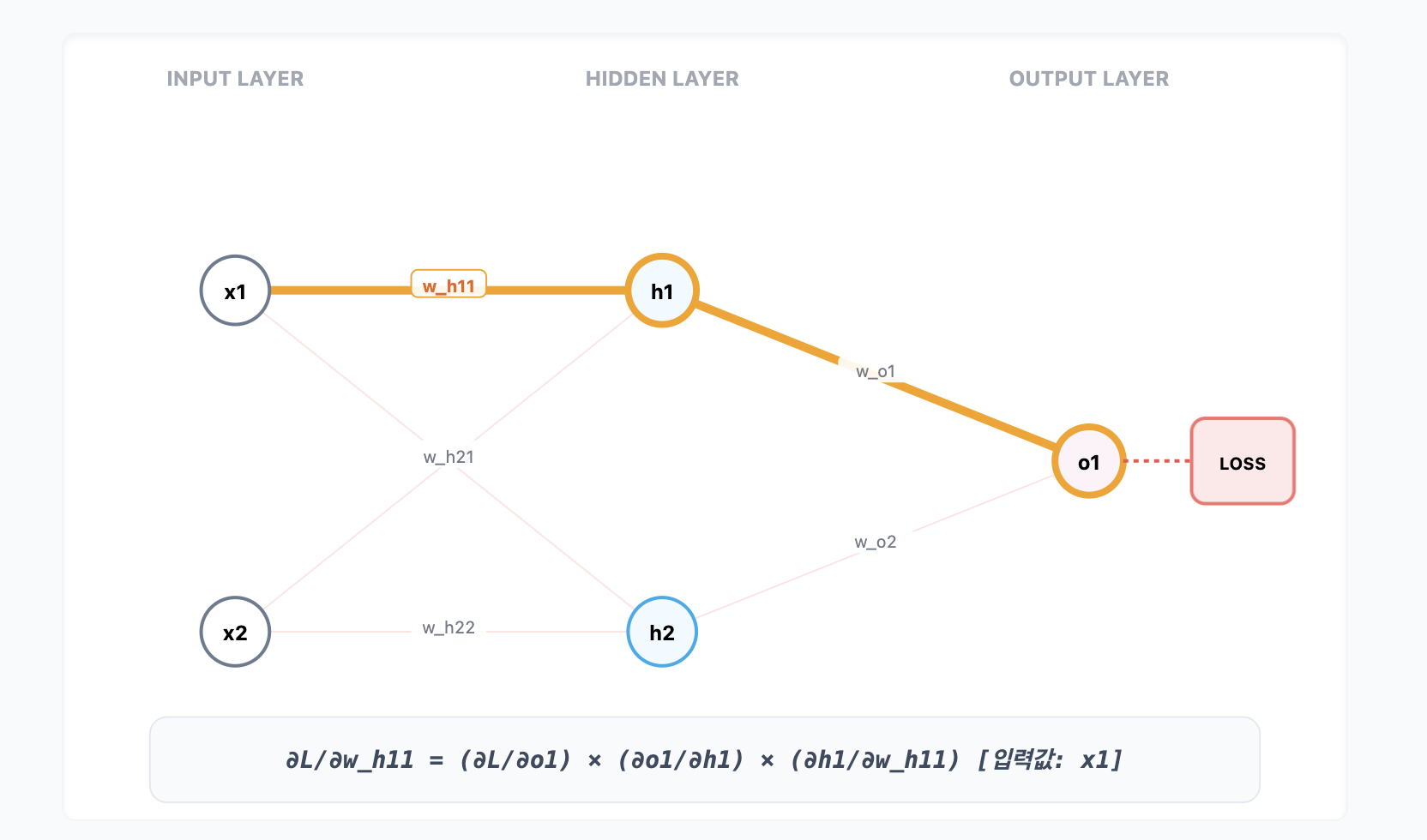
신경망에서의 체인룰 작동 원리

입력층($x$), 은닉층($h$), 출력층($o$), 그리고 손실($L$)로 구성된 네트워크를 생각해 봅시다.

함수의 입장에서 '바깥(겉)'은 계산의 가장 마지막 단계를 감싸고 있는 함수를 말합니다.

• 순전파 방향: $x \rightarrow h \rightarrow o \rightarrow L$
• 함수 중첩 형태: $L( o( h( w ) ) )$

여기서 가장 바깥쪽에서 모든 것을 감싸고 있는 껍질은 바로$L$ (손실 함수)입니다. $w$는 그 양파 속 가장 깊숙이 박혀 있는 알맹이와 같고요.

은닉층 가중치 $w_{h11}$을 업데이트하려면?

가중치 $w_{h11}$이 손실 $L$에 미치는 영향력인 $\frac{\partial L}{\partial w_{h11}}$을 구해야 합니다. 이때 오차는 다음과 같은 경로를 타고 거꾸로 흐릅니다.

[오차 전달 경로]

$$\text{Loss}(L) \rightarrow \text{Output}(o_1) \rightarrow \text{Hidden}(h_1) \rightarrow w_{h11}$$

[체인룰 수식]

$$\frac{\partial L}{\partial w_{h11}} = \underbrace{\frac{\partial L}{\partial o_1}}_{\text{1. 가장 겉껍질 (L) 미분}} \times \underbrace{\frac{\partial o_1}{\partial h_1}}_{\text{2. 중간 껍질 (o) 미분}} \times \underbrace{\frac{\partial h_1}{\partial w_{h11}}}_{\text{3. 가장 안쪽 (h) 미분}}$$

• $\frac{\partial L}{\partial o_1}$ : 가장 바깥 함수인 $L$을 미분했으니 이게 바로 겉미분입니다.
• $\frac{\partial h_1}{\partial w_{h11}}$ : 가장 안쪽에 숨어있는 $h$를 미분했으니 이게 속미분의 끝판왕인 셈이죠.
  
  

예제

1. 초기값 설정 (가정)

• 입력 데이터: $x_1 = 1, x_2 = 2$
• 가중치 (Hidden): $w_{h11} = 0.5$ (우리가 찾는 알맹이), $w_{h21} = 0.3$ (나머지는 생략하거나 고정)
• 가중치 (Output): $w_{o1} = 0.7$ (은닉층 $h_1$에서 $o_1$으로 가는 선)
• 실제 정답: $Target = 1.0$
• 오차 함수: $L = \frac{1}{2}(o_1 - Target)^2$

2. 순전파 (Forward Pass): 껍질을 덮는 과정

가장 안쪽 알맹이($w$)부터 계산되어 가장 바깥쪽($L$)으로 나아갑니다.

• 은닉 노드 $h_1$ 계산:
  $h_1 = (x_1 \times w_{h11}) + (x_2 \times w_{h21}) = (1 \times 0.5) + (2 \times 0.3) = \mathbf{1.1}$
• 출력 노드 $o_1$ 계산: (편의상 $h_2$쪽 값은 0이라 가정)
  $o_1 = (h_1 \times w_{o1}) = 1.1 \times 0.7 = \mathbf{0.77}$
• 최종 오차 $L$ 계산:
  $L = \frac{1}{2}(0.77 - 1.0)^2 = \frac{1}{2}(-0.23)^2 = \mathbf{0.02645}$

3. 역전파 (Backward Pass): 겉미분부터 속미분까지

이제 겉에서부터 안으로 파고듭니다.

 

1. [Step 1] 겉미분: $\frac{\partial L}{\partial o_1}$ (가장 바깥쪽 $L$의 껍질을 까다)
   $L$을 $o_1$으로 미분하면 $(o_1 - Target)$이 남습니다.
   • 계산: $0.77 - 1.0 = \mathbf{-0.23}$
2. [Step 2] 중간미분: $\frac{\partial o_1}{\partial h_1}$ (출력 가중치의 영향력을 확인하다)
   $o_1 = h_1 \times w_{o1}$ 이므로 $h_1$으로 미분하면 가중치 $w_{o1}$만 남습니다.
   출력값 $o_1$이 어떻게 만들어졌는지 식을 보면: $o_1 = h_1 w_{o1} + h_2 w_{o2}$ 입니다(예제에서는 편의상 $h_2$ 쪽을 0으로 두었지만, 수식에서는 존재한다고 가정합니다.)
   
   편미분의 핵심: 우리는 $h_1$이 $o_1$에 주는 영향력($\frac{\partial o_1}{\partial h_1}$)만 궁금합니다.
   따라서 $h_1$만 변수로 보고 나머지는 모두 숫자(상수)로 취급합니다.
   
   항별 미분:
   • 첫 번째 항 $(h_1 w_{o1})$을 $h_1$으로 미분 $\rightarrow$ $w_{o1}$만 남습니다.
   • 두 번째 항 $(h_2 w_{o2})$에는 $h_1$이 전혀 없으므로 $\rightarrow$ 미분하면 $0$이 됩니다.
   • 결과: $\frac{\partial o_1}{\partial h_1} = w_{o1} + 0 = \mathbf{0.7}$
   • 계산: $w_{o1} = \mathbf{0.7}$
3. [Step 3] 속미분: $\frac{\partial h_1}{\partial w_{h11}}$ (가장 안쪽 알맹이 $w_{h11}$에 도달하다)
   $h_1 = x_1 \times w_{h11} + \dots$ 이므로 $w_{h11}$로 미분하면 입력값 $x_1$만 남습니다.
   • 계산: $x_1 = \mathbf{1}$

 

최종 결합 (체인룰)

이제 세 값을 곱하면 가중치 $w_{h11}$이 오차에 준 영향력이 나옵니다.

$$\frac{\partial L}{\partial w_{h11}} = (-0.23) \times 0.7 \times 1 = \mathbf{-0.161}$$

결론: 가중치 $w_{h11}$을 살짝 키우면 오차가 줄어든다는 것을 알게 되었습니다!

왜 역전파를 사용하는가? (효율성)

만약 역전파가 없다면, 수백만 개의 가중치를 하나하나 미세하게 바꿔보며 오차를 계산해야 합니다(수치 미분). 이는 계산량이 너무 많아 불가능에 가깝습니다.

역전파는 동적 계획법(Dynamic Programming)의 원리를 활용합니다.

• 한 번 계산된 미분값을 메모리에 저장해두고 앞쪽 레이어에서 재사용합니다.
• 단 한 번의 Backward Pass로 네트워크 내의 모든 가중치의 기울기를 동시에 구할 수 있습니다.

 

참고: 위 예제는 이해를 돕기 위해 활성화 함수를 생략했습니다. 실제 신경망에서는 각 층 사이에 활성화 함수가 존재하며, 체인룰 계산 과정에 '활성화 함수의 미분값'도 함께 곱해집니다. 이때 시그모이드처럼 미분값이 작은 함수를 쓰면 층이 깊어질수록 기울기가 사라지는 '기울기 소실' 문제가 발생하는 것입니다