Batch Normalization

딥러닝 모델은 수많은 층(Layer)으로 이루어져 있습니다. 데이터가 이 층들을 통과할 때마다 값이 변하는데, 이게 쌓이다 보면 뒤쪽 층으로 갈수록 데이터가 너무 커지거나 한쪽으로 쏠려서 학습이 제대로 안 되는 문제가 생깁니다. 이를 해결하는 핵심 기술이 바로 배치 정규화입니다.

 

왜 하는가? (문제점: 내부 공변량 변화)

데이터가 층을 통과할 때마다 분포가 계속 뒤틀리는 현상을 내부 공변량 변화(Internal Covariate Shift)라고 합니다.

• 비유: 건물 1층을 지을 때마다 땅바닥이 조금씩 기우뚱하고 움직인다면 어떨까요? 위로 갈수록 건물은 엄청나게 흔들릴 것입니다.
• 배치 정규화는 각 층을 지날 때마다 흔들리는 바닥을 평평하게 다져주는 '지반 공사'와 같습니다.

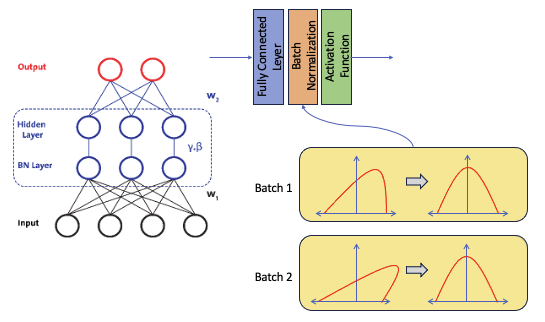
수식으로 보는 배치 정규화 4단계

논문에 나오는 수식은 복잡해 보이지만, 논리는 아주 명쾌합니다.

Input: 미니 배치 데이터 $B = \{x_1, \dots, x_m\}$

Parameters to be learned: $\gamma$ (Scale), $\beta$ (Shift)

1. 미니 배치 평균($\mu_B$) 구하기 : "중심 잡기"

$$\mu_B \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_i$$

• 데이터의 평균을 구합니다. 이 평균은 나중에 데이터에서 빼버릴 값입니다.
• 목적은 데이터의 중심을 '0'으로 옮기기 위한 준비 단계입니다.

2. 미니 배치 분산($\sigma_B^2$) 구하기 : "퍼진 정도 파악"

$$\sigma_B^2 \leftarrow \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2$$

• 데이터가 얼마나 넓게 퍼져 있는지 확인합니다. 이 값으로 데이터를 나눠서 모두의 '보폭'을 맞출 것입니다.

3. 정규화(Normalize) : "평균 0, 분산 1로 변환"

$$\hat{x}_i \leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$$

여기서 분자인 **$(x_i - \mu_B)$가 바로 '편차(Deviation)'**입니다.

• 편차 구하기: 데이터에서 평균을 빼서 중심을 0으로 보냅니다. (Zero-centering)
• 표준편차로 나누기: 데이터의 폭을 1로 통일합니다. ($\epsilon$은 0으로 나누는 것을 막는 안전장치입니다.)
• 이게 z-score이다 ..보통은 -3에서 3 사이의

4. 스케일 및 시프트(Scale and Shift) : "최적의 위치 찾기"

$$y_i \leftarrow \gamma \hat{x}_i + \beta$$

• 무조건 평균 0, 분산 1로만 두면 모델의 유연성이 떨어질 수 있습니다.
• 그래서 모델이 학습하면서 "데이터를 이만큼 키우고($\gamma$), 이만큼 이동시키는($\beta$) 게 가장 학습이 잘 되네!"라고 스스로 판단해서 미세 조정을 합니다.

 

핵심 포인트: '진짜 평균' vs '가짜 평균'이 만든 노이즈

여기서 아주 흥미로운 현상이 발생합니다. 우리가 구한 평균($\mu_B$)은 사실 전 세계 모든 데이터를 다 본 '진짜 평균'이 아닙니다.

• 미니 배치의 한계: 학습 속도를 위해 데이터를 10개, 20개씩 끊어서 보기 때문에, 우리가 구한 평균은 그 순간의 '가짜(샘플) 평균'일 뿐입니다.
• 노이즈의 연쇄 반응: * 이번 배치의 평균이 10.1이었다면, 다음 배치는 9.9가 될 수 있습니다.
  • 이렇게 평균($\mu_B$)이 매번 틀어지면, 그 값에 의존하는 분산($\sigma_B^2$)도 함께 흔들립니다.
  • 결국 최종 출력값인 $y_i$ 역시 매번 미세하게 진동하며 '노이즈'가 낀 상태가 됩니다.

💡 이 노이즈는 '약'일까, '독'일까?

놀랍게도 이 노이즈는 모델에게 약'이 됩니다! 인공지능이 데이터의 아주 미세한 특징에만 집착하는 것을 방해하여, 오히려 어떤 데이터가 들어와도 유연하게 대처하는 과적합(Overfitting) 방지 효과를 냅니다. 이를 규제(Regularization) 효과라고 부릅니다.

 

---

📈 실험 결과: Fully Connected vs. Batch Normalization

기본적인 **Fully Connected Layer(전결합층)**만 사용해도 모델은 어느 정도 학습을 해내며 나쁘지 않은 결과를 보여줍니다. 하지만 여기에 **배치 정규화(Batch Normalization)**를 추가하면 다음과 같은 뚜렷한 차이가 나타납니다.

1. 더 빠른 학습 속도 (Faster Convergence)

• 이유: 데이터가 0을 중심으로 예쁘게 정규화되어 들어오기 때문에, 가중치를 업데이트하는 방향(Gradient)이 헤매지 않고 최단 거리로 이동합니다.
• 결과: 배치 정규화가 없는 모델이 100번 반복(Epoch)해야 도달할 정확도를, 배치 정규화 모델은 20~30번 만에 달성하는 '속도 향상'을 눈으로 확인할 수 있습니다.

2. 더 높은 최종 정확도 (Higher Accuracy)

• 이유: 앞서 설명한 '착한 노이즈' 덕분입니다. 미니 배치마다 발생하는 미세한 평균/분산의 차이가 모델이 특정 데이터에만 과하게 집착하는 것(과적합)을 막아줍니다.
• 결과: 학습 데이터뿐만 아니라 처음 보는 테스트 데이터에서도 더 유연하게 정답을 맞히는 '일반화 성능'이 좋아져 최종 정확도가 상승합니다.