데이터 전처리: Normalization

머신러닝 모델을 만들 때, 서로 다른 단위(예: 수입 건수 vs 수출 금액)를 가진 컬럼들을 그대로 넣으면 모델은 숫자가 큰 컬럼이 더 중요하다고 착각하게 됩니다. 이를 해결하기 위해 데이터의 '체급'을 맞추는 과정이 바로 정규화(Normalization) 입니다.

가장 대표적인 세 가지 기법인 Starndardication, Min-Max 스케일링, 로그 변환에 대해 깊이 있게 알아보겠습니다.

 

표준화 (Standardization, Z-score Scaling)

표준화는 데이터의 평균을 0, 분산을 1로 만들어 모든 피처가 동일한 '표준적인 흩어짐'을 갖게 하는 기법입니다. 이 공식($Z = \frac{X - \mu}{\sigma}$)을 제대로 이해하기 위해 통계적 지표들을 하나씩 뜯어봅시다

분산(Variance, $\sigma^2$)의 의미

• 의미: 데이터가 평균($\mu$)으로부터 얼마나 '멀리 흩어져 있는가'를 나타내는 총량입니다.
• 수식: $\sigma^2 = \frac{\sum (X - \mu)^2}{n}$
• 왜 제곱을 하나요? 편차($X - \mu$)를 그냥 더하면 0이 되기 때문에, 마이너스 부호를 없애고 흩어진 정도를 양수로 합산하기 위해 제곱을 사용합니다.

 

편차(Deviation, $X - \mu$)

• 의미: 개별 데이터 값($X$)이 평균($\mu$)으로부터 얼마나 떨어져 있는지를 나타냅니다
• 이 값이 양수면 평균보다 크다는 뜻이고, 음수면 평균보다 작다는 뜻입니다. 표준화 공식의 분자에 위치하여 데이터의 중심을 0으로 이동시키는 역할을 합니다

 

표준편차(Standard Deviation, $\sigma$)의 의미

• 의미: 분산에 루트를 씌운 값으로, '평균적인 흩어짐의 거리'를 뜻합니다.
• 단위의 회복: 분산은 제곱을 했기 때문에 단위가 왜곡됩니다(예: $cm \rightarrow cm^2$). 여기에 루트를 씌우면 다시 원래 데이터와 같은 단위($cm$)로 돌아와, 우리가 직관적으로 "평균에서 이만큼 떨어져 있구나"라고 이해할 수 있는 '잣대'가 됩니다.

 

표준화(Standardization)의 핵심 원리

표준화 공식 $Z = \frac{X - \mu}{\sigma}$에는 데이터를 평균 0, 분산 1로 만들기 위한 두 단계의 수학적 장치가 숨어 있습니다.

• 평균을 0으로 만드는 과정: Zero-centering (중심 이동)
  공식의 분자인 편차($X - \mu$)가 이 역할을 수행합니다.
  • 원리: 모든 데이터 값에서 전체 평균($\mu$)을 빼버리는 것입니다.
  • 결과: 평균보다 컸던 값은 양수가 되고, 평균보다 작았던 값은 음수가 됩니다. 데이터들의 새로운 중심점은 자연스럽게 0으로 옮겨집니다.
  • 의미: 데이터의 절대적인 수치(예: 연봉 5,000만 원)보다 "평균보다 얼마나 높은가/낮은가"라는 상대적 차이에 집중하게 만듭니다.
• 분산(및 표준편차)을 1로 만드는 과정: Scaling (크기 조정)
  분모인 표준편차($\sigma$)로 나누는 과정이 이 역할을 수행합니다.
  • 원리: 평균이 0으로 맞춰진 데이터들을 다시 그 집단의 '평균적인 흩어짐(표준편차)'으로 나눕니다.
  • 결과: 원래 데이터의 변동 폭이 크든 작든, 모든 데이터는 '표준편차라는 보폭'으로 재정의됩니다.
    • 예를 들어, 원래 표준편차가 10이었다면 10으로 나눔으로써 새로운 표준편차는 $10/10 = 1$이 됩니다.
    • 표준편차가 1이 되면, 그 제곱인 분산($\sigma^2$) 역시 $1^2 = 1$이 됩니다.
    • 의미: 서로 다른 단위와 변동성을 가진 피처들을 '동일한 보폭'을 가진 데이터로 변환하여, 모델이 모든 피처를 공평하게 비교할 수 있게 합니다. 내가 갖진 편차가 표준편차의 몇배인가? 즉, 표준편차 개수

결과 데이터의 범위: 왜 -3 ~ 3인가요?

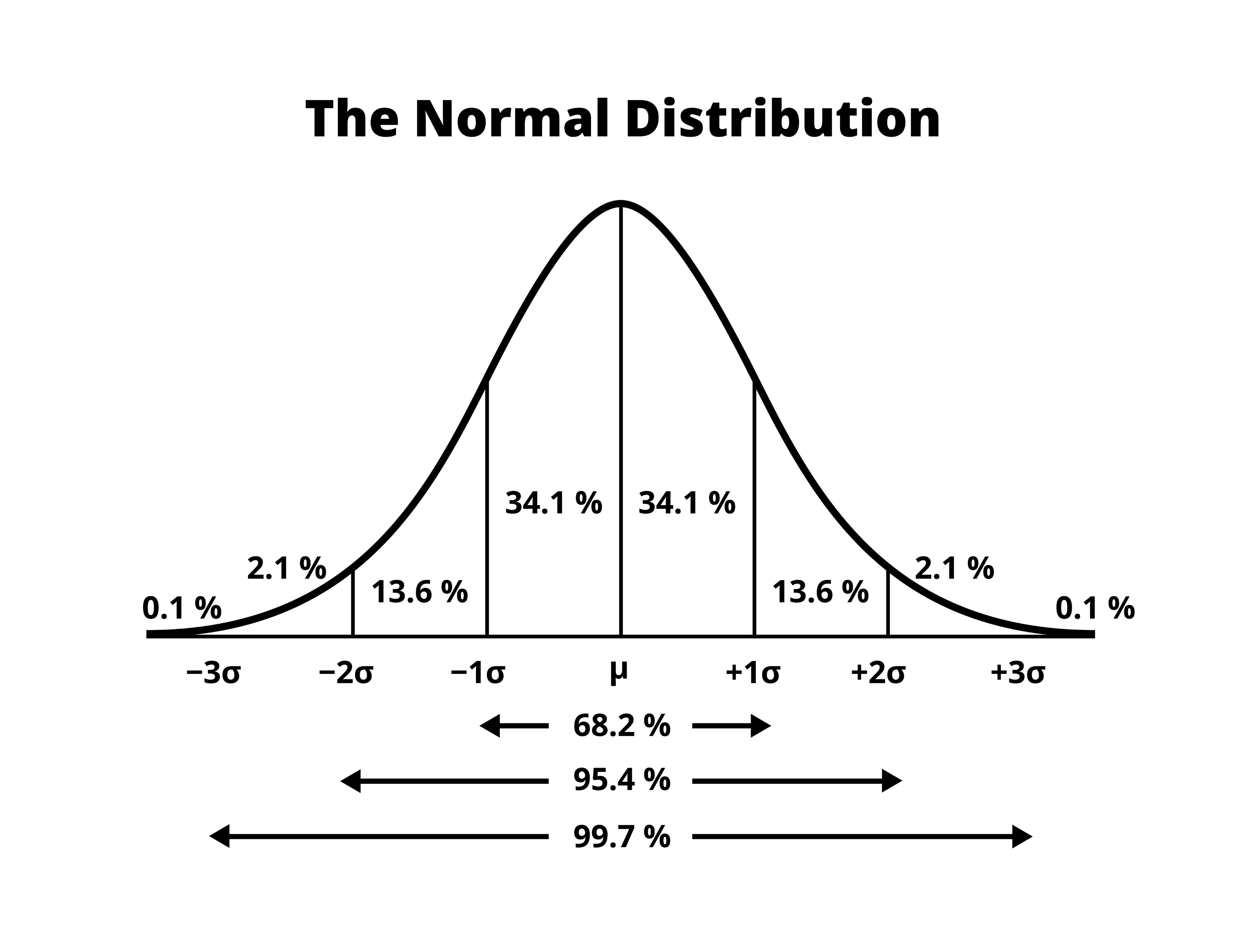
표준화된 데이터가 가우시안 정규 분포를 따른다면, 통계적으로 다음과 같은 분포를 가집니다.

• 데이터의 약 68%가 -1 ~ 1 사이에 존재
• 데이터의 약 95%가 -2 ~ 2 사이에 존재
• 데이터의 약 99.7%가 -3 ~ 3 사이에 존재

---

 Min-Max Scaling

데이터의 최솟값을 0, 최댓값을 1로 설정하여 모든 데이터를 0과 1 사이의 비율로 변환하는 기법입니다.

공식의 수학적 원리 분해

$$X_{new} = \frac{X - X_{min}}{X_{max} - X_{min}}$$

이 공식은 두 단계의 논리적인 과정을 거칩니다.

• 분자 ($X - X_{min}$): "모든 데이터의 시작점을 0으로!"
  모든 값에서 최솟값을 뺍니다. 이렇게 하면 가장 작았던 값($X_{min}$)은 0이 되고, 나머지 값들은 0으로부터 얼마나 떨어져 있는지를 나타내는 양수가 됩니다.
• 분모 ($X_{max} - X_{min}$): "데이터의 전체 길이를 1로!"
  데이터셋의 전체 범위(Range)로 나누는 과정입니다. 분자가 '0으로부터의 거리'라면, 이를 '전체 길이'로 나누어 전체 대비 어느 정도 위치에 있는지(0% ~ 100%)를 비율로 환산하는 것입니다.

"전체 길이($X_{max} - X_{min}$)라는 커다란 도화지 위에서, 내 데이터가 시작점($X_{min}$)으로부터 얼마나 멀리($X - X_{min}$) 와 있는지를 0과 1 사이의 비율로 나타낸 것"입니다.

비유: 100점 만점이 아닌 시험 점수를 %로 바꾸기

어떤 시험의 최저점이 50점이고, 최고점이 150점입니다. 당신은 100점을 받았습니다. 당신은 이 시험에서 상위 몇 % 정도일까요? 0과 1 사이로 나타내면 얼마일까요?

 

1. 분자 ($X - X_{min}$) → "바닥을 0점으로 맞추기"
   원래 최저점이 50점이니까, 이 점수 체계에서는 50점이 사실상 '꼴등(0점)'입니다.
   • 내 점수(100점)에서 최저점(50점)을 뺍니다.
   • $100 - 50 = 50$
   • 의미: 이제 내 점수는 "0점(최저점)으로부터 50점만큼 떨어져 있다"는 사실을 알게 됩니다. 이것이 '거리'입니다.
2.  분모 ($X_{max} - X_{min}$) → "전체 길이를 구하기"
   시험 점수가 퍼져 있는 전체 범위를 구합니다.
   
   • 최고점(150점)에서 최저점(50점)을 뺍니다.
   • $150 - 50 = 100$
   • 의미: 이 시험 점수의 전체 길이는 100점 폭이라는 것을 알게 됩니다. 이것이 기준이 되는 '전체 눈금'입니다.
3. 합치기 (분자 / 분모) → "전체 중 나의 위치(비율)"
   이제 내가 떨어진 거리를 전체 길이로 나눕니다.
   
   • 50/100 = 0.5
   • 의미: 모든 숫자를 100(전체 폭)으로 나누면, 가장 큰 값인 100은 1이 되고, 중간값인 50은 0.5가 됩니다
     
     

이렇게 하면 원래 데이터가 1,000만 원~5,000만 원짜리 연봉 데이터든, 1도~40도짜리 기온 데이터든 상관없이 똑같이 "최저는 0, 최고는 1, 중간은 0.5"라는 똑같은 체급(Scale)으로 변하게 됩니다. 그래서 머신러닝 모델이 "아, 얘네들은 이제 다 똑같은 비중으로 비교하면 되겠구나!"라고 이해하는 것이죠

---

로그 변환 (Log Transformation)

엄밀히 말하면 스케일링보다는 데이터 분포의 왜곡(Skewness) 을 잡고 정규성을 확보하기 위해 사용합니다
$$y = \log(x)$$

• 왜 사용하는가? 수입이나 수출 금액처럼 '작은 값은 많고 큰 값은 아주 적은' 오른쪽으로 꼬리가 긴 데이터($Right-Skewed$)를 처리할 때 필수적입니다.
• 작동 원리: 로그 함수는 작은 숫자의 차이는 크게 벌리고, 큰 숫자의 차이는 아주 좁게 만듭니다.
  • $\log(10) = 1, \log(100) = 2, \log(1000) = 3$ 처럼 숫자가 커질수록 값의 증가 폭을 확 줄여버립니다.
• 효과: 극단적인 값(Outlier)의 영향력을 줄여 데이터 분포를 종 모양인 정규 분포에 가깝게 만듭니다. 선형 회귀 모델 등 정규성을 가정하는 모델에서 성능 향상에 매우 효과적입니다.
• 주의점: $0$이나 음수에는 로그를 취할 수 없습니다. 데이터에 0이 포함된 경우 보통 $x+1$을 해주는 $y = \log(x + 1)$ 함수를 사용합니다.

실전 예제 

어느 회사의 연봉 데이터가 다음과 같다고 가정해 봅시다. 대부분의 직원은 3,000만 원~7,000만 원을 받지만, 사장님 한 명이 100억 원을 받습니다.

• 일반 직원 A: 4,000만 원
• 일반 직원 B: 5,000만 원
• 사장님: 10,000,000만 원 (100억)

이 데이터를 그대로 그래프로 그리면, 사장님의 연봉이 너무 커서 일반 직원들의 데이터는 0 근처에 아주 작게 뭉쳐 보이게 됩니다. 머신러닝 모델 입장에서도 이 '사장님' 데이터 때문에 전체 평균이 왜곡되어 제대로 된 학습이 어려워집니다.

 

수학적으로 로그는 "큰 숫자는 작게 만들고, 작은 숫자의 차이는 유지"하는 성질이 있습니다. 상용로그($\log_{10}$)를 기준으로 계산해 볼까요?

• 100만 원 $\rightarrow \log_{10}(10^6) = \mathbf{6}$
• 1,000만 원 $\rightarrow \log_{10}(10^7) = \mathbf{7}$
• 1억 원 $\rightarrow \log_{10}(10^8) = \mathbf{8}$
• 100억 원 $\rightarrow \log_{10}(10^{10}) = \mathbf{10}$

---

💡 정리하며: 어떤 것을 선택할까?

기법	주요 특징	추천 상황
Standardization	평균 0, 분산 1로 변환	이상치가 있거나 가우시안 분포인 경우
Min-Max Scaling	0 ~ 1 사이로 압축	데이터의 범위를 제한해야 할 때 (딥러닝 등)
Log Transformation	큰 값을 억제하고 정규성 확보	데이터가 한쪽으로 심하게 치우친 경우