분류 모델의 성능 성적표, ROC 곡선과 AUC

머신러닝 모델을 만들고 나면 "이 모델이 얼마나 잘 분류하고 있는가?"를 판단해야 합니다. 단순히 정확도(Accuracy)만 보기에는 데이터가 불균형할 때 위험할 수 있죠. 이때 가장 널리 쓰이는 시각화 도구가 바로 ROC 곡선(Receiver Operating Characteristic Curve)입니다.

 

ROC(Receiver Operating Characteristic Curve) 곡선은 Confusion Matrix 수치를 활용해, 분류기의 분류 능력을 그래프로 표현하는 방법입니다.
물론 이 그래프도 PR 커브와 마찬가지로 분류기의 Threshold 값의 변화에 따라 Confusion Matrix에 생기는 변화로 인해 그려지는 것입니다.

• 배경: 모델은 보통 0~1 사이의 확률값을 내놓습니다. 이때 "0.5 이상이면 양성(1)이다"라고 정하는 기준이 임계값입니다. 이 기준을 0.1로 낮추거나 0.9로 높일 때마다 모델의 성적표가 달라지는데, 그 궤적을 그린 것이 ROC입니다.

ROC 곡선의 핵심 구성 요소

ROC 곡선을 이해하려면 먼저 오차 행렬(Confusion Matrix)에서 파생된 세 가지 지표를 알아야 합니다.

 

TPR (True Positive Rate, 참 양성률)

• 다른 이름: 민감도(Sensitivity), 재현율(Recall)
• 의미: 실제 양성($TP+FN$)인 데이터 중 모델이 양성($TP$)이라고 제대로 맞춘 비율
  $$TPR = \frac{TP}{TP + FN}$$

TNR(True Negative Rate,참 음성률)

• 다른 이름: 특이도(Specificity)
• 의미: 실제 음성($FP+TN$)인 데이터 중 모델이 음성($TN$)이라고 제대로 맞춘 비율
  $$TNR = Specificity = \frac{TN}{FP + TN}$$

FPR (False Positive Rate, 위양성률)

• 의미: 실제 음성($FP+TN$)인 데이터 중 모델이 양성($FP$)이라고 잘못 예측한 비율
  $$FPR = \frac{FP}{FP + TN} = 1 - Specificity$$

---

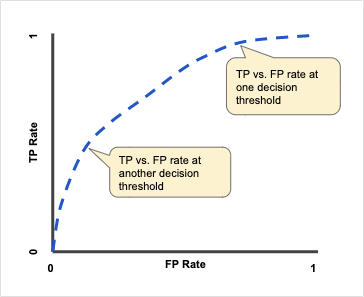
임계값(Threshold)의 변화와 궤적

모델은 '확률값'을 내뱉습니다. 우리가 이 임계값을 조정함에 따라 TPR과 FPR은 마치 시소처럼 움직입니다.

• 임계값을 낮추면 (예: 0.1): 웬만하면 다 양성이라고 판단합니다. 진짜 양성을 놓치지 않으니 TPR은 올라가지만, 그만큼 가짜 양성도 많아져서 FPR도 함께 올라갑니다. (그래프의 오른쪽 상단으로 이동)
• 임계값을 높이면 (예: 0.9): 아주 확실한 것만 양성이라고 판단합니다. 틀릴 확률은 줄어들어 FPR은 낮아지지만, 진짜 양성을 놓칠 확률이 커져 TPR도 낮아집니다. (그래프의 왼쪽 하단으로 이동)

이 임계값을 0에서 1까지 변화시키며 기록한 TPR과 FPR의 자취가 바로 ROC 곡선입니다.

 

ROC 곡선은 왼쪽 상단 모서리에 바짝 붙을수록 좋은 모델입니다.

• 완벽한 모델: FPR은 0이면서 TPR은 1인 지점(좌상단 꼭짓점)을 지납니다.
• 쓸모없는 모델 (Random): 45도 직선($y=x$) 형태입니다. 동전 던지기와 다를 바 없는 무작위 예측을 의미합니다.

AUC (Area Under the Curve)

AUC는 ROC 곡선 아래의 면적을 정적분으로 계산한 값입니다. 수학적으로는 모델이 무작위로 선택된 양성 샘플을 무작위로 선택된 음성 샘플보다 높게 점수 매길 확률과 같습니다.

$$AUC = \int_{0}^{1} TPR(FPR^{-1}(x)) \, dx$$

 

정량적 비교의 편의성 (Quantification)

여러 개의 모델을 개발했을 때, 어떤 모델이 더 우수한지 그래프 모양만 보고 판단하기는 어렵습니다.

• 두 모델의 ROC 곡선이 서로 교차한다면? 시각적으로는 우열을 가리기 힘듭니다.
• 이때 AUC라는 스칼라(Scalar) 값으로 변환하면, 0.85와 0.82처럼 명확한 수치 비교가 가능해집니다.

임계값(Threshold)으로부터의 자유 (Threshold-Invariance)

정확도(Accuracy)는 특정 임계값(예: 0.5)에서의 성능만 보여줍니다. 하지만 AUC는 모든 가능한 임계값에서의 성능을 통합해서 계산합니다.

• "이 모델은 임계값을 어디로 잡든 간에 전반적으로 분류 능력이 좋은가?"를 평가하는 척도가 됩니다.
• 모델의 '잠재력' 자체를 평가하는 지표라고 할 수 있습니다.

 

 

📊 ROC-AUC vs PRC-AP 

구분	ROC (Receiver Operating Characteristic)	PRC (Precision-Recall Curve)
X축	FPR (False Positive Rate)	Recall (재현율 = TPR)
Y축	TPR (민감도 = Recall)	Precision (정밀도)
요약 지표	AUC (면적 값)	AP (Average Precision)
무작위 모델	AUC = 0.5	AP = 양성 클래스의 비율 $\frac{Positive}{Total}$
주요 관심사	전체적인 판별 능력 (양성/음성 모두 중요)	양성 클래스를 얼마나 잘 찾아내는가

 

ROC 곡선과 AUC

• 특징: 실제 음성(Negative) 중 양성으로 잘못 예측한 비율(FPR) 대비 진짜 양성을 맞춘 비율(TPR)을 봅니다.
• 장점: 양성과 음성의 비율이 비슷할 때 모델의 전반적인 분류 능력을 평가하기에 매우 표준적입니다.
• 한계: 데이터 불균형(예: 음성이 99%)이 심할 경우, $FPR$의 분모인 음성 데이터($TN + FP$)가 너무 커서 $FPR$ 값이 매우 작게 유지됩니다. 이로 인해 모델 성능이 실제보다 좋아 보이는 '낙관적 편향'이 발생할 수 있습니다.

PR 곡선과 AP

• 특징: 정밀도(Precision)와 재현율(Recall)의 관계를 그래프로 나타냅니다.
• AP (Average Precision): PR 곡선 아래의 면적을 계산한 값으로, 모든 임계값에서의 정밀도 평균치를 의미합니다.
• 장점: 불균형 데이터(Imbalanced Data)에서 빛을 발합니다. 음성 데이터가 아무리 많아도 정밀도는 오직 '양성으로 예측한 것($TP+FP$)'만 분모로 삼기 때문에, 가짜 양성($FP$)에 매우 민감하게 반응하여 모델의 실제 성능을 더 엄격하게 평가합니다.

 

💡 언제 무엇을 써야 할까요?

✅ ROC-AUC를 선택할 때

• 데이터 내 양성(1)과 음성(0)의 비율이 비슷할 때.
• 양성을 놓치는 것($FN$)과 음성을 오해하는 것($FP$)의 위험도가 비슷할 때.
• 예: 일반적인 스팸 메일 분류.

✅ PRC-AP를 선택할 때

• 양성 데이터가 매우 적은 불균형 데이터일 때.
• 양성 클래스를 정확히 찾아내는 것이 훨씬 중요할 때.
• 예: 희귀 질병 진단(암), 신용카드 부정 결제 탐지(Fraud), 물체 검출(Object Detection).