Loss, Accuracy and Metric

인공지능 모델을 학습시킬 때 우리는 "정확도(Accuracy)가 99%인 모델을 만들고 싶다"고 말합니다. 하지만 정작 모델을 학습시키는 코드를 보면 loss='cross_entropy'처럼 우리가 원하는 '정확도'와는 조금 다른 수치를 줄이려고 노력합니다.

오늘은 컴퓨터를 위한 채찍(Loss)과 사람을 위한 성적표(Metric), 그리고 학습의 단위인 에포크(Epoch)에 대해 그래프와 함께 깊이 있게 파헤쳐 보겠습니다.

 

 

Loss vs Metric : 채찍과 성적표

Loss (손실 함수): "컴퓨터를 위한 채찍"

• 정의: 모델이 얼마나 '틀렸는지'를 하나의 숫자로 요약해서 보여주는 지표
• 역할: 최적화(Optimization). 컴퓨터는 이 Loss 값을 줄이는 방향으로 가중치(weight)를 계속 수정합니다.
• 특징:
  • 반드시 미분이 가능해야 합니다. (기울기를 따라 내려가며 학습해야 하기 때문)
  • 값이 작을수록 모델이 정답에 가깝게 예측하고 있다는 뜻입니다.
• 예시: $MSE$ (회귀), $Cross-Entropy$ (분류)

크로스 엔트로피(Cross-Entropy)는 간단히 말해 "두 확률 분포가 얼마나 다른지"를 측정하는 지표입니다.
머신러닝의 분류(Classification) 문제에서 모델이 예측한 확률 값이 실제 정답(Label)과 얼마나 차이가 나는지를 계산할 때 가장 많이 사용됩니

Metric (평가 지표): "사람을 위한 성적표"

• 정의: 학습이 완료된 모델을 사람이 직관적으로 판단하기 위해 사용하는 숫자입니다.
• 역할: 평가(Evaluation). "이 모델을 실제로 쓸 수 있는 수준인가?"를 결정하는 잣대가 됩니다.
• 특징:
  • 미분이 불가능해도 상관없습니다. 사람이 이해하기 쉬운 것이 가장 중요합니다.
  • 비즈니스 목표에 따라 여러 개를 동시에 보기도 합니다.
• 예시: $RMSE$, $MAE$, $Accuracy$, $F1-Score$

Accuracy (정확도): "가장 대표적인 Metric"

• 정의: 전체 데이터 중 모델이 정답을 맞힌 비율입니다.
• 공식:
  $$Accuracy = \frac{정답을\ 맞힌\ 개수}{전체\ 데이터\ 개수}$$
• 특징:
  • 분류 문제에서 가장 직관적인 성능 지표입니다.
  • 왜 Loss로 쓰지 않나요? 정확도는 "맞혔다/틀렸다"로만 계산되므로 그래프가 계단식입니다. 즉, 특정 지점에서 미분값이 0이 되어 컴퓨터가 어느 방향으로 학습해야 할지 알 수 없기 때문에 Metric으로만 주로 사용됩니다.

 

📊 Loss vs Metric vs Accuracy 한눈에 비교

구분	Loss (손실 함수)	Metric (평가 지표)	Accuracy (정확도)
누가 보나?	컴퓨터 (학습용)	사람 (판단용)	사람 (직관적 확인)
필수 조건	미분 가능해야 함	직관적이어야 함	(Metric의 일종)
주요 목적	가중치 업데이트 (최적화)	모델 성능의 객관적 검증	전체적인 분류 성공률 파악
예시	Log Loss, MSE	RMSE, F1-Score	"정확도 98%"

 

---

왜 Metric(정확도)을 Loss로 쓰면 안 될까?

궁극적인 목표가 정확도(Accuracy)라면, 정확도를 직접 줄이는 방향으로 학습하면 되지 않을까요? 하지만 여기에는 몇 가지 기술적인 문제가 있습니다.

 

• Accuracy (계단식 그래프):"
  • 정확도는 "맞혔다/틀렸다"로 계산되므로 그래프가 계단식(Step function) 형태를 띱니다.
    경사하강법(Gradient Descent)을 쓰려면 미분을 통해 기울기를 구해야 하는데, 정확도는 대부분의 지점에서 기울기가 0이라 학습이 불가능합니다.특정 지점에서 미분값이 0이 되거나 정의되지 않기 때문에, 컴퓨터가 어느 방향으로 가중치를 수정해야 할지 알 수 없습니다.
  • 값의 급격한 변동: Metric은 값이 툭툭 끊겨 변하는 경향이 있어 최적화 과정이 매끄럽지 못하고, 국소 최적점(Local Minimum)에 빠지거나 발산할 위험이 큽니다.
  • 적합(Overfitting) 위험: Metric에만 과도하게 최적화하면 모델이 학습 데이터에만 매몰될 수 있습니다
• Loss (매끄러운 곡선): 반면 $Cross-Entropy$ 같은 손실 함수는 확률 값을 사용하여 매끄러운 곡선을 만듭니다. 덕분에 아주 미세한 변화도 감지하여 컴퓨터가 학습할 방향(기울기)을 찾을 수 있게 해줍니다.

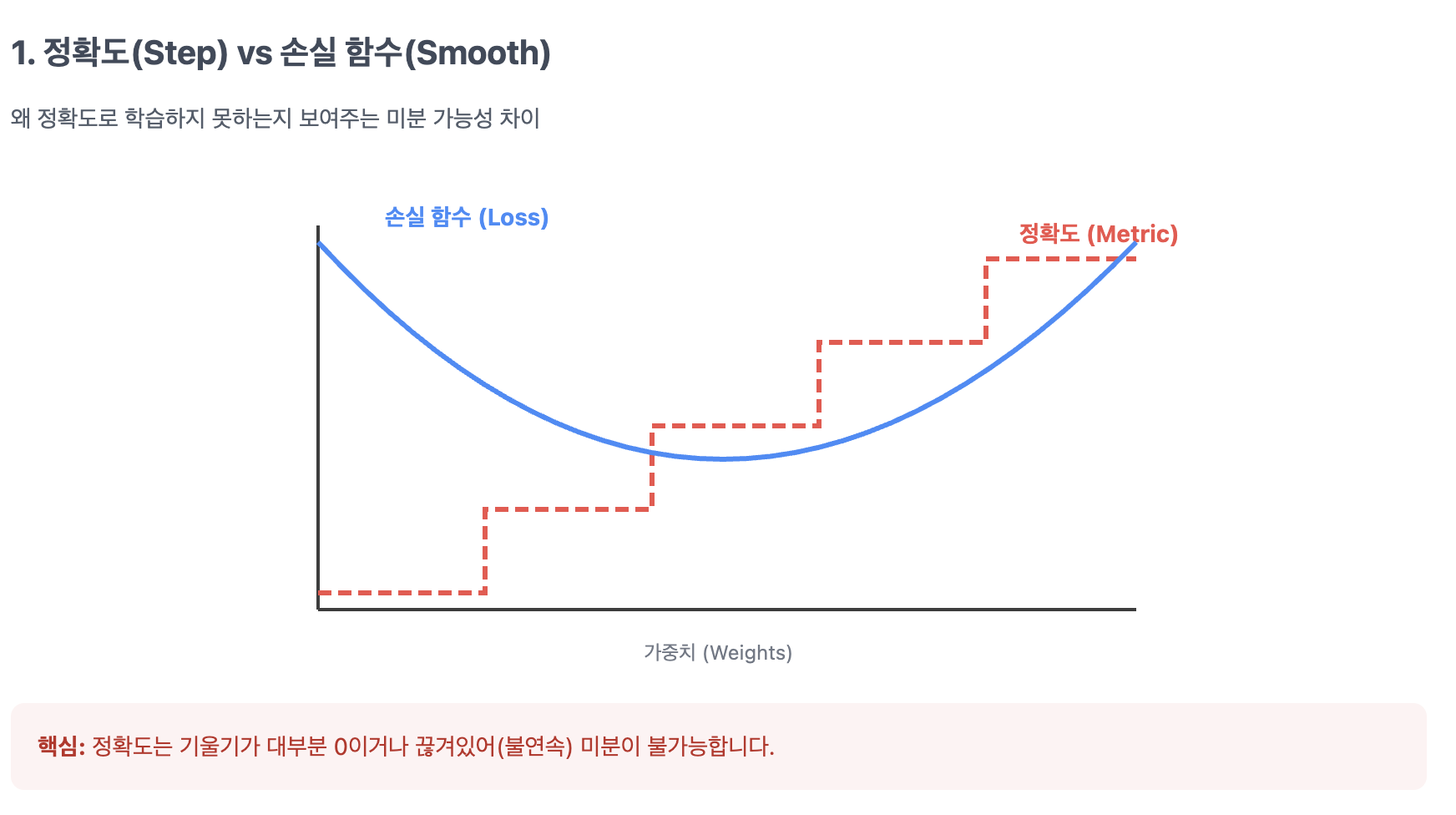
따라서 우리는 미분 가능하고 연속적인 Cross-Entropy나 $MSE$ 같은 Loss 함수를 따로 사용하는 것입니다.

 

Loss와 Accuracy의 미묘한 관계 (역설적 상황)

일반적으로 Loss가 감소하면 Accuracy는 증가합니다. 하지만 항상 그런 것은 아닙니다.

위 예시처럼 Loss는 증가했는데 Accuracy는 오히려 상승하는 경우가 발생합니다. 왜 그럴까요?

• 측정 대상의 차이: Cross-Entropy는 정답 레이블에 얼마나 가까운 '확률'로 예측했는지를 봅니다. 반면 Accuracy는 특정 임계값을 넘었는지(이진화)만 따집니다.
• 연속 vs 이산: Loss는 정답 확률이 0.7에서 0.5로 떨어지면 즉각 반응하지만, Accuracy는 0.5만 넘으면 여전히 '정답'으로 간주하여 변화가 없을 수 있습니다.

---

Train Loss vs Val Loss

학습이 진행됨에 따라 우리는 훈련 손실(Train Loss)과 검증 손실(Validation Loss)의 추이를 지켜봐야 합니다. 여기서 모델의 운명이 결정됩니다. 두 지표는 수학적으로 완전히 똑같은 공식(예: Cross-Entropy)을 사용합니다. 차이는 오직 '대상 데이터'에 있습니다.

• Train Loss (훈련 손실): 모델이 직접 보고 공부하는 데이터(Train Set)에 대한 오차입니다. 모델은 이 오차를 줄이기 위해 가중치를 수정(Update)합니다.
• Validation Loss (검증 손실): 모델이 학습 중에 절대 보지 않은 데이터(Validation Set)에 대한 오차입니다. 이 오차로는 가중치를 수정하지 않습니다. 오직 '감시'만 할 뿐이죠.

💡 비유하자면?

• Train Loss: "문제집의 연습 문제를 풀었을 때 틀린 정도" (답지를 보고 다시 공부함)
• Val Loss: "교과서 밖 기출 문제를 풀었을 때 틀린 정도" (자신의 실력을 가늠만 함)

📊 손실 곡선(Loss Curve) 분석

1. 과소적합 (Underfitting): 학습 초기, 두 Loss가 모두 높은 상태입니다. 모델이 아직 데이터의 패턴을 파악하지 못했습니다.
2. 이상적인 학습 (Good Fit): 두 Loss가 함께 매끄럽게 감소합니다. 연습 문제(Train)도 잘 풀고 실전(Val) 실력도 늘고 있는 상태입니다.
3. 과적합 (Overfitting): 위 그래프의 특정 지점 이후를 보세요. Train Loss는 계속 떨어지는데 Val Loss는 다시 올라갑니다. 모델이 연습 문제를 통째로 외워버려서 실전 응용력이 떨어지는 상태입니다.
   • Tip: 검증 손실이 다시 올라가기 직전, 가장 낮은 지점이 바로 우리가 학습을 멈춰야 할 최적의 시점입니다.

 

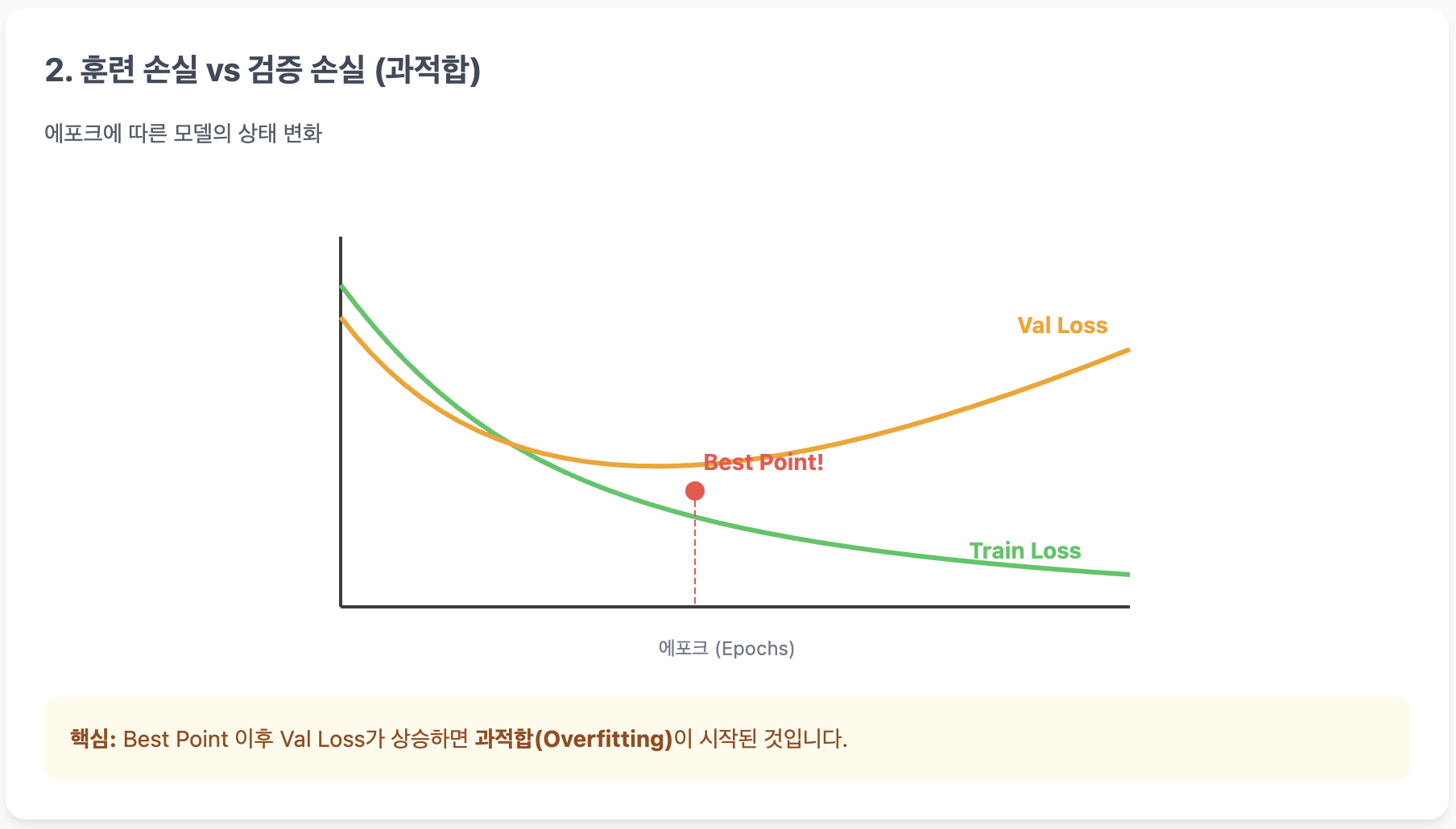
에포크(Epoch)와 학습의 단위

학습을 시작하면 Epoch 1/100 같은 로그가 뜹니다. 여기서 용어 정리를 한번 하고 가겠습니다.

• 에포크(Epoch): 준비된 전체 데이터를 딱 한 번 모두 훑어본 상태 (문제집 1회독)
• 배치 사이즈(Batch Size): 한 번에 학습할 데이터의 묶음 단위 (한 번에 10문제씩 풀기)
• 이터레이션(Iteration): 한 에포크 내에서 가중치를 업데이트하는 횟수

 

결론: 문제에 맞는 직관이 실력이다

분류 모델에서는 Accuracy가 우월한 Metric이지만, 모델을 깎아 만드는 '도구'로는 Cross-Entropy가 훨씬 적당합니다.
반면 회귀 모델에서는 $RMSE$가 Loss와 Metric 양쪽 모두로 효과적으로 사용되기도 하죠.

우리가 해결해야 할 Task에 따라 어떤 함수를 Loss로 쓰고 어떤 지표를 Metric으로 볼지 결정하는 '직관력'이 딥러닝 엔지니어의 핵심 역량입니다.