오차와 편차의 차이부터 RMSE의 진짜 의미까지

머신러닝을 공부하다 보면 '틀렸다'는 말을 참 다양하게 표현합니다. 오차, 편차, 손실, 지표... 비슷해 보이지만 쓰임새가 완전히 다릅니다. 이 글 하나로 완벽하게 정리해 보겠습니다.

 

오차(Error) vs 편차(Deviation) vs 분산(Variance): 기준의 차이

가장 먼저 정복해야 할 개념입니다. 핵심은 "무엇을 기준으로 뺏는가?"입니다.

• 오차 (Error): "정답(Actual)"과의 차이입니다. 모델이 얼마나 정확한지를 말할 때 씁니다.
  $오차 = 실제값 - 예측값$
• 편차 (Deviation): "평균(Mean)"과의 차이입니다. 데이터가 얼마나 퍼져 있는지를 말할 때 씁니다.
  $편차 = 데이터값 - 평균값$
• 분산(Variance): "데이타가 평균에서 얼마나 멀리 떨어져서 퍼져있는가?", 분산은 '편차들의 제곱'을 모두 더해 평균을 낸 값, 불안정성(Instability): 결과가 얼마나 널뛰는가?
  $분산 = E[편차^2]$

💡 한 줄 요약: 오차는 '정확도'의 문제이고, 편차는 '분포', 분산은 안정성

 

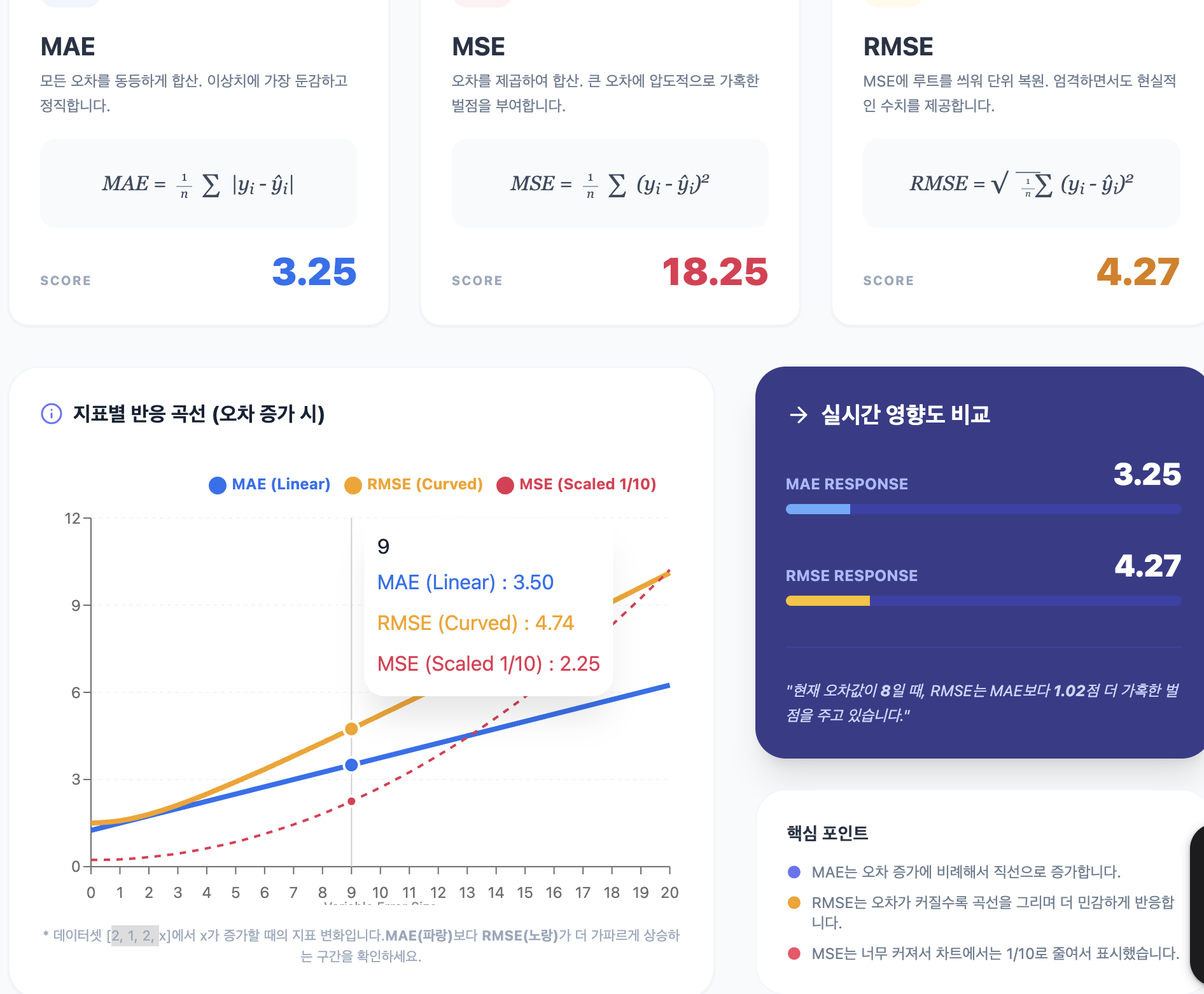
MAE (Mean Absolute Error) : 오차의 평균을 있는 그대로

MAE는 가장 직관적인 지표입니다. "예측이 평균적으로 실제값과 얼마나 차이가 나는가?"를 단순히 숫자로 보여줍니다.

• Absolute (절대값): 오차가 +1만 원이든 -1만 원이든, '틀린 거리' 자체를 보기 위해 절대값을 씌웁니다.
• Mean (평균): 그 거리들의 평균을 냅니다.

삼성전자 주가 예시로 돌아가 볼까요?

내가 "10만 원"이라고 예측했는데 실제가 "9만 원"이라면, 오차는 1만 원입니다. 다음 날 "9만 원"이라 예측했는데 실제가 "10만 원"이어도 오차는 (절대값 덕분에) 똑같이 1만 원입니다. 이틀간의 평균 오차(MAE)는 1만 원이 됩니다.

$$MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|$$

 

만약 주식 가격을 예측했는데 결과가 이렇다면:

• 1일차: 실제 100원, 예측 110원 (오차 10)
• 2일차: 실제 200원, 예측 195원 (오차 5)
• 3일차: 실제 150원, 예측 150원 (오차 0)

1. 오차를 다 더하면: $10 + 5 + 0 = 15$
2. 데이터가 3개니까 3으로 나누기: $15 \div 3 = 5$
3. 결론: MAE는 5 (평균적으로 5원 정도 틀린다!)

 

MSE(Mean Squared Error): "컴퓨터가 좋아하는 지표"

오차를 그냥 더하지 않고 제곱해서 평균을 낸 값입니다.

$$MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$$

• 왜 제곱을 할까요? 1. 음수(-) 부호를 없애줍니다.
• 수학적으로 미분이 매끄럽게 잘 되어 컴퓨터가 오차를 줄이는 방향으로 학습(경사하강법)하기에 최적입니다.
• 특징: 오차가 크면 클수록 제곱값이 기하급수적으로 커집니다. 그래서 큰 오차에 매우 민감하게 반응합니다.
• 단점: 단위가 '제곱'이 되어버려(예: 원 → 원²) 사람이 직관적으로 "얼마나 틀렸네"라고 이해하기 어렵습니다.

 

RMSE: 큰 오차에 엄격한 점수

RMSE(Root Mean Square Error)는 복잡해 보이지만, 사실 "예측이 실제와 얼마나 틀렸나?"를 나타내는 점수, 즉 오차의 크기값입니다.

"예측값이 실제값에서 평균적으로 얼마나 떨어져 있는가"로도 말할수 있습니다.

예를 들어, 내일 삼성전자 주가를 맞히는 인공지능을 만든다고 해볼게요.

1. Error (오차): 내가 "10만 원"이라고 예측했는데 실제가 "9만 원"이라면, 오차는 1만 원입니다.
2. Square (제곱): 오차가 +1만 원일 수도 있고 -1만 원일 수도 있죠? 이 부호를 없애고 계산하기 편하게 제곱을 합니다.
3. Mean (평균): 하루만 맞히는 게 아니라 열흘 동안의 평균 오차를 냅니다.
4. Root (루트): 아까 제곱을 해서 숫자가 너무 커졌으니, 다시 원래 단위(원)로 되돌리기 위해 루트를 씌웁니다.

결론: RMSE가 1,000이라면, "이 모델은 평균적으로 1,000원 정도 틀리네"라고 이해하시면 됩니다. 숫자가 작을수록 정확한 모델이겠죠? 

$$RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}$$

 

• $n$ : 데이터의 총 개수 (Sample Size)
  • 의미: 내가 예측을 시도한 전체 데이터의 횟수입니다.
  • 설명: "시험을 총 몇 번 봤는지", "며칠 동안 주가를 예측했는지"와 같은 전체 관측치의 개수입니다. 이 숫자로 나누기 때문에 '평균'의 의미가 생깁니다.
• $y_i$ : 실제값 (Actual Value / Ground Truth)
  • 의미: 실제로 일어난 정답입니다.
  • 블로그용 설명: "실제 오늘 삼성전자 주가", "실제 시험 점수"처럼 우리가 맞히고자 하는 진짜 데이터입니다.
• $\hat{y}_i$ (y-hat) : 예측값 (Predicted Value)
  • 의미: 모델(AI)이 계산해서 내놓은 예측 결과입니다.
  • 블로그용 설명: 인공지능이 "오늘 주가는 이럴 거야"라고 예상한 값입니다. 알파벳 위에 삿갓 모양(^)이 씌워져 있어 '햇(hat)'이라고 읽습니다. 통계학에서 이 삿갓 기호는 보통 '추정치(예상치)'를 의미합니다.

 

💡 수식을 말로 풀어서 쓰면?

이 수식을 순서대로 읽으면 블로그 독자들이 훨씬 이해하기 쉽습니다.

1. $(y_i - \hat{y}_i)$: [오차] 정답에서 내 예측을 뺀다.
2. $(...)^2$: [제곱] 마이너스(-)가 나오지 않게 제곱한다. (틀린 거리가 멀수록 벌점이 커짐!)
3. $\sum_{i=1}^{n}$: [합계] 1번 데이터부터 $n$번 데이터까지 위에서 계산한 오차들을 다 더한다.
4. $\frac{1}{n}$: [평균] 다 더한 값을 개수($n$)로 나누어 평균을 낸다. (MSE)
5. $\sqrt{...}$: [루트] 제곱해서 커진 숫자에 루트를 씌워 원래 단위로 되돌린다. (RMSE)

 

 

 

 

x는 이상치값, 만약 x가 10이라면

$$\frac{1}{4} \times (|2| + |1| + |2| + |10|) = \frac{15}{4} = 3.75$$

 

 

특성                           MAE                                              MSE                                               RMSE

오차의 크기에 대한 민감도	덜 민감(모든 오차를 동등하게 처리)	더 민감(큰 오차에 더 큰 가중치 부여)	더 민감 (큰 오차에 더 큰 가중치 부여)
이상치에 대한 민감도	덜 민감 (이상치의 영향을 상대적으로 적게 받음)	더 민감 (이상치로 인해 값이 크게 증가할 수 있음)	더 민감 (이상치로 인해 값이 크게 증가할 수 있음)
오차의 단위와 해석	오차의 단위와 동일, 해석이 직관적임.	원래 데이터의 단위와 다름, 해석이 덜 직관적임.	오차의 단위와 동일, 해석이 직관적임.

 

마무리: 어떤 상황에 어떤 지표를 쓸까?

 

• MAE
  • 모든 오차를 동등하게 취급 (직관적)
  • 이상치(Outlier)가 있어도 무난한 성능을 원할 때,둔감
• RMSE 
  • 큰 오차를 민감하게 잡아내고 싶을 때 (이상치에 엄격함)
  • "사람의 최애 지표" (Metric으로 주로 사용)
  • 단위(Unit)를 맞춰줍니다. 예를 들어 주가를 맞히는데 오차가 '1,000원'이라면, MSE는 '1,000,000원²'이 됩니다. '원 제곱'이라는 단위는 우리가 이해할 수 없죠. 여기에 다시 루트를 씌워주면 '1,000원'이라는 익숙한 단위
• MSE
  • 오차를 있는 그대로 평균 내고 싶을 때 (직관적임)
  • 이상치에 대해 매우 민감
  • 컴퓨터의 최애 지표" (Loss로 주로 사용) - 루트가 없어서 미분이 쉽습니다
• 결론:
  • "모델이 얼마나 틀렸나?"를 사람에게 설명할 때는 MAE나 RMSE(Metric)를 보여주세요.
  • "모델을 어떻게 학습시킬까?"를 고민한다면 MSE(Loss)를 최적화하세요.